Bibliography

Bg

Bergman, G. M.: The Diamond Lemma for Ring Theory. Advances in Math. 29 (1978), 178-218.

BW

Birman, J., Wenzl, H,: Braids, Link Polynomials and a new Algebra. Tansactions of the Amer. Math. Soc., Vol. 313, No. 1 (1989), 249-273.

CP

Chari, V., Pressley, A.: A Guide to Quantum Groups. Cambridge University Press. 1994.

Co

De Concini C.: Symplectic Standard Tableaux. Advances in Mathematics 34 (1979), 1-27.

DD

Dipper, R., Donkin, S.: Quantum 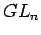$GL_n$. Proc. London Math. Soc. 63 (1991), 165-211.

DJ

Dipper, R., James, G.: The 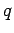$q$-Schur Algebra. Proc. London Math. Soc. (3) 59 (1989), 23-50.

DJ2

Dipper, R., James, G.: 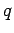$q$-tensor space and 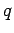$q$-Weyl modules, Trans. A.M.S. 327 (1991), 251-282.

DJM

Dipper, R., James, G., Mathas, A.: Cyclotomic 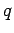$q$-Schur Algebras. Math. Zeitschrift 229 (1998), 385-416.

Do1

Donkin, S.: Good Filtrations of Rational Modules for Reductive Groups. Arcata Conf. on Repr. of Finite Groups. Proceedings of Symp. in Pure Math., Vol. 47 (1987), 69-80.

Do2

Donkin, S.: Representations of symplectic groups and the symplectic tableaux of R.C. King. Linear and Multilinear Algebra, Vol. 29 (1991), 113-124.

Dt

Doty, S.: Polynomial Representations, Algebraic Monoids, and Schur Algebras of Classical Type. J. of Pure and Applied Algebra, 123 (1998), 165-199.

GL

Graham, J.J., Lehrer, G.I.: Cellular Algebras. Invent. Math. 123 (1996), 1-34.

Gr

Green, J.A.: Combinatorics and the Schur algebra. J. of Pure and Appl. Alg. 88 (1993), 89-106.

GR

Green, R.M.: 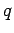$q$-Schur algebras and quantized enveloping algebras. Thesis. University of Warwick, 1995.

HH

Hashimoto, M., Hayashi, T.: Quantum Multilinear Algebra. Tohoku Math. J., 44 (1992), 471-521.

Ha2

Hayashi, T.: Quantum Deformation of Classical Groups. Publ. RIMS, Kyoto Univ. 28 (1992), 57-81.

Ha1

Hayashi, T.: Quantum Groups and Quantum Determinants. J. of Algebra 152 (1992), 146-165.

Ki

King, R.C.: Weight multiplicity for classical groups., Group Theoretical Methods in Physics (fourth International Colloquium, Nijmegen 1975), Lecture Notes in Physics 50, Springer 1975.

KX

König, S., Xi, C.: On the structure of cellular algebras. Algebras and Modules II, Proceedings of ICRA VIII (Geiranger), CMS Conference Proceedings.

Ma

Martin, S.: Schur Algebras and Representation Theory. Cambridge University Press, 1993.

O1

Oehms, S.: Symplektische 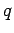$q$-Schur-Algebren, Thesis, University of Stuttgart. Shaker Verlag Aachen, 1997.

O2

Oehms, S.: Centralizer Coalgebras, FRT-Construction and Symplectic Monoids. J. of Algebra 244 (2001), 19-44.

RTF

Reshetikhin, N. Y., Takhtajan, L. A., Faddeev, L. D.: Quantization of Lie groups and Lie algebras, Leningrad Math. J. 1 (1990), 193-225.

Tk

Takhtajan, L.A.: Lectures on Quantum Groups. In: Introduction to Quantum Group and Integrable Massive Models of Quantum Field Theory (Hrsg.: M.-L. Ge, B.-H. Zhao. World Scientific, 1990.

We

Wenzl, H.: Quantum Groups and Subfactors of Type B, C and D. Commun. Math. Phys. 133 (1990), 383-432.