We prove a more general statement concerning elements
![]() defined similar to the elements
defined similar to the elements ![]() of
section 14. For the set of subsets
of
section 14. For the set of subsets
![]() which have
which have ![]() elements we will write
elements we will write
![]() . We set
. We set
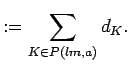
The more general statement of 13.1 reads:
Let
![]() .
If
.
If
![]() is a partition of
is a partition of
![]() into disjoint
subsets
into disjoint
subsets ![]() and
and ![]() then to each
then to each
![]() there is an integer
there is an integer
![]() such that
such that
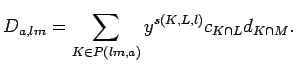
We will prove this by induction on ![]() . If
. If ![]() and
and ![]() then
then
![]() and there is no
and there is no
![]() .
If
.
If ![]() we have
we have
![]() and
and ![]() . Thus
. Thus
![]() leads to a solution.
leads to a solution.
For the induction step we first consider the case ![]() and calculate
and calculate
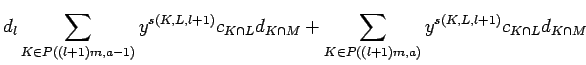 |
||
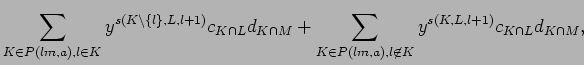 |
Setting
![]() leads to a solution. If
leads to a solution. If ![]() we
apply relation (14) of the exterior algebra to obtain
we
apply relation (14) of the exterior algebra to obtain
Now, in a similar way as in the proof of Lemma 14.1 we see that
![]() where
where
![]()
![]() .
Since
.
Since
![]() we obtain
we obtain
![]() . Thus, setting
. Thus, setting
![]() if
if ![]() and
and
![]() elsewise
leads to a solution.
elsewise
leads to a solution.
It remains to check that
![]() if
if
![]() .
More generally we prove that
.
More generally we prove that
Since
![]() the assertion follows in the first case. Next we consider
the assertion follows in the first case. Next we consider
![]() .
Here we have
.
Here we have
and the assertion follows since
![]() . Finally we have to consider
. Finally we have to consider ![]() . From the calculation
above we get
. From the calculation
above we get
which directly gives the result.