Bibliography

Br

Brauer, R.: On Algebras which are connected with the semisimple continuous Groups. Annals of Math. Vol. 38, No. 4 (1937), 857-871.

Co

De Concini C.: Symplectic Standard Tableaux. Advances in Mathematics 34 (1979), 1-27.

Do1

Donkin, S.: On Schur Algebras and Related Algebras I, Journal of Algebra 104 (1986), 310-328.

Do2

Donkin, S.: Good Filtrations of Rational Modules for Reductive Groups. Arcata Conf. on Repr. of Finite Groups. Proceedings of Symp. in Pure Math., Vol. 47 (1987), 69-80.

Do3

Donkin, S.: Representations of symplectic groups and the symplectic tableaux of R.C. King. Linear and Multilinear Algebra, Vol. 29 (1991), 113-124.

Dt

Doty, S.: Polynomial Representations, Algebraic Monoids, and Schur Algebras of Classical Type. J. of Pure and Applied Algebra 123 (1998), 165-199.

GL

Graham, J.J., Lehrer, G.I.: Cellular Algebras. Invent. Math. 123 (1996), 1-34.

Gg

Grigor'ev, D. J.: An Analogue of the Bruhat Decomposition for the Closure of the Cone of a Chevalley Group of the Classical Series. Soviet Math. Dokl., Vol. 23 (1981), No. 2.

Ha

Hayashi, T.: Quantum Deformation of Classical Groups. Publ. RIMS, Kyoto Univ. 28 (1992), 57-81.

Ia

Iano-Fletcher, M.: Polynomial Representations of Symplectic Groups. Thesis, University of Warwick, 1990.

Ki

King, R.C.: Weight multiplicity for classical groups., Group Theoretical Methods in Physics (fourth International Colloquium, Nijmegen 1975), Lecture Notes in Physics 50, Springer 1975.

Ma

Manin, Y.I.: Quantum Groups and Non-Commutative Geometry. CRM, Univesitè de Montrèal, 1988.

Mr

Martin, S.: Schur Algebras and Representation Theory. Cambridge University Press, 1993.

Oe

Oehms, S.: Symplektische 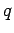$q$-Schur-Algebren, Thesis, University of Stuttgart.

RTF

Reshetikhin, N. Y., Takhtadjian, L. A., Faddeev, L. D.: Quantization of Lie groups and Lie algebras, Leningrad Math. J. 1 (1990), 193-225.

Su

Sudbery, A.: Matrix-Element Bialgebras Determined by Quadratic Coordinate Algebras. J. of Algebra, Vol 158, (1993), 375-399.

Ta

Takeuchi, M.: Matric Bialgebras and Quantum Groups. Israel J. of Math., Vol. 72, Nos. 1-2, (1990), 232-251.

We

Wenzl, H.: On the structure of Brauer's centalizer algebras. Annals of Math., 128 (1988), 173-193.