First, some considerations about the exterior algebra
are needed. It is easy to see and well known
that this graded ![]() -algebra is a
comodule algebra for the bialgebra
-algebra is a
comodule algebra for the bialgebra ![]() , i.e. it is an
, i.e. it is an ![]() -comodule such that multiplication is a
morphism of comodules. In fact, the homogenous summands
-comodule such that multiplication is a
morphism of comodules. In fact, the homogenous summands
![]() of
of
![]() are comodules for the coalgebras
are comodules for the coalgebras ![]() . Since
. Since
![]() is an epimorphic image of
is an epimorphic image of ![]() the exterior
algebra is a comodule algebra for the latter one, as well.
the exterior
algebra is a comodule algebra for the latter one, as well.
As usual we write
![]() for the residue class of
for the residue class of
![]() in
in
![]() and denote arbitrary multiplications by
and denote arbitrary multiplications by
![]() , too. For a subset
, too. For a subset
![]() ordered
ordered
![]() by the given order
by the given order
![]() on
on ![]() (called an ordered subset in the sequel)
we use the abbreviation
(called an ordered subset in the sequel)
we use the abbreviation
![]() . The elements
. The elements ![]() give a basis of
give a basis of
![]() if
if ![]() ranges over all
subsets of
ranges over all
subsets of ![]() . A basis for
. A basis for
![]() is obtained when
is obtained when ![]() ranges over all
subsets of cardinality
ranges over all
subsets of cardinality ![]() , the collection of which will be denoted by
, the collection of which will be denoted by
![]() . The comodule structure of
. The comodule structure of
![]() can be described in a
simple way using bideterminants for the partition
can be described in a
simple way using bideterminants for the partition
![]() . These are just the usual
. These are just the usual ![]() -minor determinants.
Denoting the structure map by
-minor determinants.
Denoting the structure map by
![]() (we will use the same symbol in
the case
(we will use the same symbol in
the case
![]() later on) we explicitly have
later on) we explicitly have
where
![]() and
and
![]() are the multi-indices corresponding to the
ordered subsets
are the multi-indices corresponding to the
ordered subsets
![]() and
and
![]() ,
respectively.
Define
,
respectively.
Define
![]() and
and
![]() for a
subset
for a
subset
![]() of cardinality
of cardinality ![]() .
Again, we write
.
Again, we write ![]() for the collection of all such subsets
for the collection of all such subsets ![]() .
Note that the
.
Note that the ![]() are in the center of the exterior algebra and in particular
commute with each other. Thus
are in the center of the exterior algebra and in particular
commute with each other. Thus ![]() is defined
independent of the order of the elements of
is defined
independent of the order of the elements of ![]() . Set
. Set

and let ![]() be the ideal in
be the ideal in
![]() generated by the elements
generated by the elements
![]() . One crucial point in the proof of
proposition 7.3 is to show that
the elements
. One crucial point in the proof of
proposition 7.3 is to show that
the elements ![]() are invariant under the bialgebra
are invariant under the bialgebra
![]() .
But first, let us establish a prototype straightening algorithm inside
the graded algebra
.
But first, let us establish a prototype straightening algorithm inside
the graded algebra
![]() with respect to the set
with respect to the set
![]() . We call an ordered subset
. We call an ordered subset
![]() symplectic if the corresponding multi-index
symplectic if the corresponding multi-index ![]() is
is
![]() -symplectic standard.
-symplectic standard.
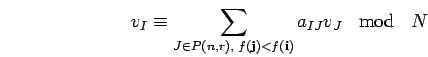
PROOF: We follow [Do3].
Clearly, we may reduce to the case
![]() since
since
![]() and the canonical isomorphism
therein respects the basis elements
and the canonical isomorphism
therein respects the basis elements ![]() and the ideal
and the ideal ![]() .
If
.
If
![]() then in
then in
![]() we calculate as in [Do3], 2.2.
we calculate as in [Do3], 2.2.
In the case
![]() this implies
this implies ![]() .
Set
.
Set
![]() and
and ![]() .
It follows from (18) that the equation
.
It follows from (18) that the equation
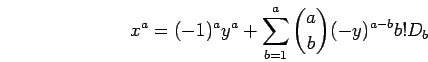
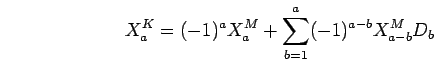
The proof can be finished now in a similar way to the proof of the
Symplectic Carter-Lusztig Lemma in [Do3]:
Since ![]() is not symplectic there is a number
is not symplectic there is a number
![]() such that
such that
![]() contains an element
contains an element ![]() satisfying
satisfying
![]() if
if ![]() or
or ![]() if
if ![]() . We assume
. We assume ![]() to be
as small as possible with this property.
Let
to be
as small as possible with this property.
Let
![]() be the unique numbers with
be the unique numbers with
![]() and
and
![]() . By minimality of
. By minimality of ![]() we have
we have ![]() . On the other hand,
. On the other hand,
![]() implies
implies ![]() .
This gives
.
This gives
![]() , that is
, that is ![]() and
and ![]() .
.
Now let
![]() be the ordered subset of the first
be the ordered subset of the first
![]() entries of
entries of ![]() and
and
![]() be the set of all
be the set of all
![]() such that both
such that both ![]() and
and ![]() are contained in
are contained in ![]() . Setting
. Setting
![]() and
and
![]() we obtain
we obtain
![]() since the elements
since the elements ![]() are in the
center of
are in the
center of
![]() . Therefore, by equation (19)
it remains to show that for all subsets
. Therefore, by equation (19)
it remains to show that for all subsets
![]() which
do not intersect
which
do not intersect ![]() we have
we have
![]() where
where
![]() is the multi-index corresponding to the ordered set
is the multi-index corresponding to the ordered set
![]() . Since
. Since
![]() if
if ![]() or
or
![]() contains an
element of
contains an
element of ![]() we further may assume
we further may assume
![]() .
Now, suppose
.
Now, suppose
![]() . Let
. Let ![]() be the set of all
be the set of all
![]() such that
such that ![]() or
or ![]() lies in
lies in ![]() . Since
. Since
![]() the intersection of
the intersection of ![]() and
and ![]() is empty, as well.
This gives a contradiction
is empty, as well.
This gives a contradiction
for ![]() and
and ![]() are disjoint subsets of
are disjoint subsets of ![]() by assumption on
by assumption on
![]() . Thus, the largest element
. Thus, the largest element ![]() of
of
![]() must be greater than
must be greater than ![]() , whereas all
elements of
, whereas all
elements of ![]() are smaller or equal to
are smaller or equal to ![]() . If
. If
![]() and
and
![]() it follows that
it follows that ![]() and
and
![]() for
for ![]() . By definition of our order on
. By definition of our order on
![]() this
means
this
means
![]() completing the proof.
completing the proof.![]()
As mentioned before, the crucial point in the proof of proposition 7.3 is contained in the following
PROOF: In the case ![]() this easily follows from (15) using the
relations given by the set
this easily follows from (15) using the
relations given by the set ![]() defined in (14). If we could divide by
defined in (14). If we could divide by
![]() , we would be able to finish the proof right now using
, we would be able to finish the proof right now using
![]() and the fact that multiplication is a morphism of
and the fact that multiplication is a morphism of
![]() -comodules. But, as this is not possible in general (note,
that we don't know if
-comodules. But, as this is not possible in general (note,
that we don't know if
![]() is a free
is a free ![]() -module, yet)
we have to proceed in another way. We set
-module, yet)
we have to proceed in another way. We set ![]() and
and
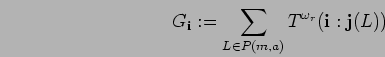
where ![]() is the multi-index corresponding to the ordered
subset
is the multi-index corresponding to the ordered
subset
![]() of
of ![]() . If
. If ![]() is the
multi-index corresponding to the ordered subset
is the
multi-index corresponding to the ordered subset
![]() we also
write
we also
write
![]() . By (17)
we have
. By (17)
we have
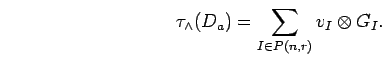
If
![]() is a
multi-index and
is a
multi-index and ![]() we set
we set
![]() . Since the result is clear in the case
. Since the result is clear in the case ![]() we know
we know
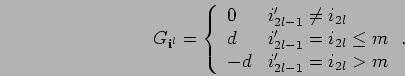
Therefore, the element
![]() is zero
or
is zero
or ![]() depending on
depending on ![]() . Let us investigate this in more
detail. If
. Let us investigate this in more
detail. If
![]() denotes the involution defined by
denotes the involution defined by
![]() for
for
![]() and
and ![]() the
centralizer of
the
centralizer of ![]() in
in ![]() , then clearly
, then clearly
![]() if and only if
if and only if
![]() for all
for all ![]() . The group
. The group ![]() is isomorphic to the Weyl group of type
is isomorphic to the Weyl group of type ![]() . It is
a semi-direct product of the normal subgroup
. It is
a semi-direct product of the normal subgroup ![]() consisting of all
consisting of all
![]() which permute neighboured pairs together
with
which permute neighboured pairs together
with ![]() , the
subgroup generated by the transpositions
, the
subgroup generated by the transpositions ![]() for
for
![]() .
.
![]() is isomorphic to
is isomorphic to ![]() , whereas the group
, whereas the group ![]() can be
identified with
can be
identified with
![]() . Choose a set
. Choose a set ![]() of left coset
representatives for
of left coset
representatives for ![]() in
in ![]() the element representing
the element representing ![]() itself being
itself being
![]() .
.
Now, if ![]() corresponds to an ordered set
corresponds to an ordered set ![]() for some
for some
![]() the inequality
the inequality
![]() holds for a permutation
holds for a permutation
![]() if and only if
if and only if
![]() . Thus, for
. Thus, for ![]() we have
we have
![]() if
if
![]() and
and
![]() . If there is no
. If there is no ![]() such that
such that ![]() one
clearly has
one
clearly has
![]() for all
for all ![]() .
Therefore, the proof is finished
as soon as we have shown
.
Therefore, the proof is finished
as soon as we have shown
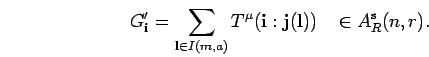
On the other hand, using Laplace Duality (see for example [Mr] 2.5.1) we calculate
Therein, note that ![]() is precisely the column stabilizer of the
basic tableaux
is precisely the column stabilizer of the
basic tableaux
![]() , whereas the column stabilizer
of
, whereas the column stabilizer
of
![]() is all of
is all of ![]() (here
(here
![]() ). Also, note that
). Also, note that ![]() is a set of left
coset representatives of
is a set of left
coset representatives of ![]() and that all permutations of
and that all permutations of ![]() are even.
Furthermore, in the right-hand-side equation we have used the
commutativity between the
are even.
Furthermore, in the right-hand-side equation we have used the
commutativity between the ![]() -determinant factors of
-determinant factors of
![]() . Now, the proof of
(20) can be reduced to the verification of
. Now, the proof of
(20) can be reduced to the verification of
To this claim we associate to a multi-index
![]() its
contents
its
contents
![]() which is defined by
which is defined by
![]() . It is
a composition of
. It is
a composition of ![]() into
into ![]() parts, that is an
parts, that is an ![]() -tuple of non negative
integers
-tuple of non negative
integers ![]() summing up to
summing up to ![]() . These compositions count the
set of
. These compositions count the
set of ![]() -orbits in
-orbits in ![]() .
Denoting the set of all such
compositions by
.
Denoting the set of all such
compositions by ![]() we can write down the right-hand term in
(22) as a sum of subsums
we can write down the right-hand term in
(22) as a sum of subsums
![]() each of which is given by
each of which is given by
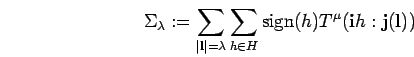
Now, the subsum
![]() (for
(for
![]() )
is just the left-hand-side in
(22). Therefore, it remains to show that all other
subsums are zero. To this claim we denote the cardinality
of the standard Young subgroup
)
is just the left-hand-side in
(22). Therefore, it remains to show that all other
subsums are zero. To this claim we denote the cardinality
of the standard Young subgroup
![]() of
of ![]() corresponding to the composition
corresponding to the composition
![]() by
by
![]() . If
. If
![]() is the unique multi-index
with contents
is the unique multi-index
with contents ![]() and
and
![]() (the initial index corresponding to
(the initial index corresponding to ![]() )
then
)
then
![]() is just the stabilizer of
is just the stabilizer of
![]() in
in ![]() . Identifying
. Identifying ![]() with
with ![]() it is the stabilizer of
it is the stabilizer of
![]() in
in ![]() .
Applying (21) again we obtain
.
Applying (21) again we obtain
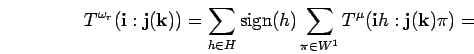
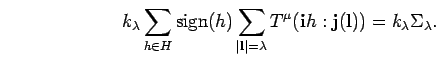
Now,
![]() must be zero since
must be zero since
![]() implies that
implies that ![]() contains at least one
number twice. We obtain
contains at least one
number twice. We obtain
![]() and because
this equation is already valid in the free
and because
this equation is already valid in the free ![]() -module
-module
![]() we conclude
we conclude
![]() for all
for all
![]() completing the proof.
completing the proof.![]()
Let us prove proposition 7.3 in
the case
![]() first. Take
first. Take
![]() . Using the classical
straighening algorithm 7.2 we may
assume
. Using the classical
straighening algorithm 7.2 we may
assume
![]() (observe that
(observe that
![]() implies
implies
![]() ). This means,
that
). This means,
that ![]() is a multi-index corresponding to a non symplectic ordered set
is a multi-index corresponding to a non symplectic ordered set
![]() in the sense of lemma
in the sense of lemma ![]() . Application of the latter one yields
. Application of the latter one yields
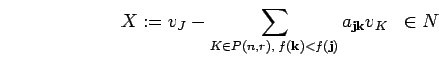
According to proposition 8.2
![]() must be
contained in
must be
contained in
![]() where
where ![]() denotes the
ideal in
denotes the
ideal in
![]() generated by
generated by ![]() . Applying (17)
we obtain the following equation in
. Applying (17)
we obtain the following equation in
![]() :
:
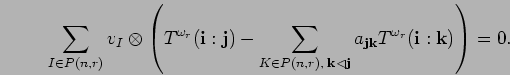
Since
![]() is a basis of
is a basis of
![]() each
individual summand in the summation over
each
individual summand in the summation over ![]() must be zero.
This gives the desired result in the case of multi-indices
must be zero.
This gives the desired result in the case of multi-indices ![]() corresponding to ordered subsets
corresponding to ordered subsets
![]() , that is
, that is
![]() . The general case for
. The general case for ![]() can be
deduced from this, easily (see [Oe], 3.11.4).
can be
deduced from this, easily (see [Oe], 3.11.4).
Now, lets turn to the general case of ![]() . Again, we may assume
. Again, we may assume
![]() by the classical
straightening algorithm. Let
by the classical
straightening algorithm. Let
![]() be the dual partition (
be the dual partition (![]() ). We spilt
). We spilt ![]() into
into ![]() multi-indices
multi-indices
![]() where for
each
where for
each
![]() the entries of
the entries of ![]() are taken from the
are taken from the ![]() -th
column of
-th
column of
![]() . The same thing can be done with
. The same thing can be done with
![]() . Since
. Since ![]() is not
is not ![]() -symplectic standard but standard
there must be a column
-symplectic standard but standard
there must be a column ![]() such that
such that ![]() is not
is not
![]() -symplectic standard. Applying the result to the
known case of
-symplectic standard. Applying the result to the
known case of
![]() we obtain
we obtain
Therein,
![]() satisfies
satisfies
![]() ,
,
![]() is constructed from
is constructed from ![]() replacing the
entries of
replacing the
entries of ![]() by that of
by that of ![]() and
and
![]() is
the same as
is
the same as
![]() for the corresponding
for the corresponding ![]() .
One easily checks
.
One easily checks
![]() and the proof of 7.3
is completed.
and the proof of 7.3
is completed.