Let
![]() be a noetherian integral domain and
be a noetherian integral domain and
![]()
![]() an invertible
element. Let
an invertible
element. Let
![]() be a free
be a free
![]() -module of rank
-module of rank ![]() . Fix a basis
. Fix a basis
![]() and let
and let
![]() denote the corresponding basis of matrix units for
denote the corresponding basis of matrix units for
![]()
![]() .
We will define two endomorphisms
.
We will define two endomorphisms
![]() and
and
![]() on
on
![]() identifying
identifying
![]() with
with
![]() (we write simply
(we write simply ![]() instead of
instead of
![]() if no
ambiguity can arise). Some additional notation is needed. We set
if no
ambiguity can arise). Some additional notation is needed. We set
and
![]()
![]() Further,
Further,
![]()
![]() defines an involution on
defines an involution on
![]()
![]() . Thus
. Thus
The following definition is taken from [Ha2, Equation (4.3),(4.5)]
(resp. [Ha1, section 5]) using the transformation
![]() and
and
![]() .
.
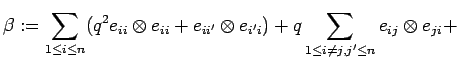
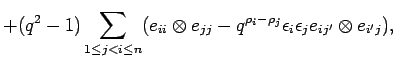
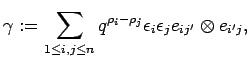
There are slightly more general versions of these endomorphisms
involving additional parameters. We may omit them without loss
of generality (see [O1, Satz 2.5.8]).
The operators ![]() and
and ![]() are related to each other by the
equation (cf. [Ha2, Equation (4.4)])
are related to each other by the
equation (cf. [Ha2, Equation (4.4)])
For
![]() write
write
![]() . A multi-index is a
map
. A multi-index is a
map
![]()
![]() frequently denoted as an
frequently denoted as an ![]() -tuple
-tuple
![]() where
where
![]() . The set of
all such multi-indices will be denoted by
. The set of
all such multi-indices will be denoted by
![]() .
We define
.
We define
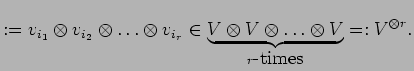
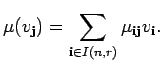
Let
![]()
![]() be the
free algebra generated by the
be the
free algebra generated by the ![]() symbols
symbols ![]() for
for
![]() . This is a graded algebra;
an
. This is a graded algebra;
an ![]() -basis of the
-basis of the ![]() -th homogeneous part
-th homogeneous part
![]() is the set
is the set
To simplify notation we introduce a new convention to write down
frequently used
elements of ![]() and its quotients in a convenient way.
For an endomorphism
and its quotients in a convenient way.
For an endomorphism ![]() on
on
![]() we write
we write
This definition can be linearly extended to all of
![]() . The
following rules are easily checked.
. The
following rules are easily checked.
We will denote the residue classes of ![]() in any quotient of
in any quotient of
![]() by
by
![]() . The
residue class
. The
residue class
![]() of
of
![]() then clearly has a similar expression in the
then clearly has a similar expression in the
![]() as the
as the
![]() do in the
do in the ![]() . The above introduced convention will be used
for
. The above introduced convention will be used
for
![]() accordingly.
accordingly.
The object of our investigations is given by the following definition:
Here the brackets
![]() denote the ideal generated by the enclosed
elements and
denote the ideal generated by the enclosed
elements and
![]() are the endomorphisms on
are the endomorphisms on
![]() defined above.
Since this ideal in the definition is homogeneous, the algebra
defined above.
Since this ideal in the definition is homogeneous, the algebra
![]() is again graded.
Here,
is again graded.
Here,
![]() is the
is the ![]() -linear span of the elements
-linear span of the elements
![]() for
for
![]() .
The algebra
.
The algebra
![]() can be identified
with a generalized
can be identified
with a generalized ![]() -construction with respect to the subset
-construction with respect to the subset
![]() denoted
denoted
![]() in [O2, section 5].
It has been pointed out there
that it possesses the
structure of a bialgebra where comultiplication and augmentation
on the generators
in [O2, section 5].
It has been pointed out there
that it possesses the
structure of a bialgebra where comultiplication and augmentation
on the generators
![]() are given by
are given by
In particular, the homogeneous summands
![]() are subcoalgebras.
Furthermore, the tensor space
are subcoalgebras.
Furthermore, the tensor space
![]() is an
is an
![]() (resp.
(resp.
![]() )-(right-)comodule. The structure map
)-(right-)comodule. The structure map
![]() is defined by
is defined by
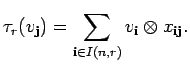
Now, if ![]() is an invertible element in
is an invertible element in ![]() , the endomorphism
, the endomorphism
![]() is known to be in the algebraic span of
is known to be in the algebraic span of ![]() ; explicitly
one has
; explicitly
one has
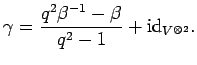
On the other hand, if ![]() is not invertible we really need to add the
relations
is not invertible we really need to add the
relations
![]() .
For instance, it has been proved in [O2, Corollary 6.2] that,
setting
.
For instance, it has been proved in [O2, Corollary 6.2] that,
setting ![]() , the bialgebra
, the bialgebra
![]() is the coordinate ring of the symplectic monoid scheme
is the coordinate ring of the symplectic monoid scheme
![]() which is defined by
which is defined by
Here, ![]() is the Gram-matrix of the canonical
skew bilinear form, that is
is the Gram-matrix of the canonical
skew bilinear form, that is
![]() where
where
![]() . The regular
function
. The regular
function
![]()
![]() is
called the coefficient of dilation (cf. [Dt]).
On the other hand,
in this case the bialgebra of the usual FRT-construction
equals
is
called the coefficient of dilation (cf. [Dt]).
On the other hand,
in this case the bialgebra of the usual FRT-construction
equals
![]() , the
commutative polynomial ring in the
, the
commutative polynomial ring in the ![]() , which is just the
coordinate ring of the monoid scheme
, which is just the
coordinate ring of the monoid scheme
![]() of
of
![]() -matrices.
Consequently the bialgebra of the usual FRT-construction
contains
-matrices.
Consequently the bialgebra of the usual FRT-construction
contains ![]() -torsion elements considered over the
ground ring
-torsion elements considered over the
ground ring
![]() of integer
Laurent polynomials in
of integer
Laurent polynomials in ![]() .
.
Let us write down a couple of consequent relations holding in
![]() .
For this purpose the algebraic span of the
.
For this purpose the algebraic span of the
![]() -endomorphisms
-endomorphisms
in
![]() will be denoted by
will be denoted by
![]() (for all
(for all ![]() ).
According to [O2, section 1, 5]
in
).
According to [O2, section 1, 5]
in
![]() the following relations hold for all
the following relations hold for all ![]() :
:
The reader should also note that by [O2, Lemma 2.2] all elements
of
![]() must be morphisms of
must be morphisms of
![]() -comodules.
-comodules.