Let
![]() be positive integers and
be positive integers and
![]() denote the set of
compositions of
denote the set of
compositions of ![]() into
into ![]() parts. These are
parts. These are ![]() -tuples
-tuples
![]() of non-negative integers
of non-negative integers
![]() summing up to
summing up to ![]() . To each composition
. To each composition
![]() there corresponds a parabolic subgroup in the symmetric
group
there corresponds a parabolic subgroup in the symmetric
group
![]() , called the standard Young
subgroup. We will denote it by
, called the standard Young
subgroup. We will denote it by
![]() . It is the subgroup
fixing the sets
. It is the subgroup
fixing the sets
![]() .
Now, let
.
Now, let
![]() be given by a reduced expression
be given by a reduced expression
![]() , where the
, where the
![]()
![]() are the simple
transpositions. We define endomorphisms
are the simple
transpositions. We define endomorphisms
for ![]() and set
and set
![]() for
for ![]() . It is easy
to see that this definition is independent of the choice of the
reduced expression for
. It is easy
to see that this definition is independent of the choice of the
reduced expression for ![]() since any two of them
can be transformed into each other using the braid relations. But
since any two of them
can be transformed into each other using the braid relations. But
![]() satisfies the quantum
Yang-Baxter equation which is just the second type braid relation
satisfies the quantum
Yang-Baxter equation which is just the second type braid relation
in the case ![]() . The latter one obviously implies the relations for
. The latter one obviously implies the relations for ![]() ,
whereas the first type braid relations
,
whereas the first type braid relations
![]() for
for
![]() hold trivially. Observe that
hold trivially. Observe that
where
![]() denotes the length of
denotes the length of ![]() , that is the number
of transpositions
in a reduced expression. Setting
, that is the number
of transpositions
in a reduced expression. Setting
![]()
![]() and using our notation
(2) we associate a quantum symplectic bideterminant
to each triple consisting of a composition
and using our notation
(2) we associate a quantum symplectic bideterminant
to each triple consisting of a composition ![]() of
of ![]() and a pair of
multi-indices
and a pair of
multi-indices
![]() by
by
The equality therein follows from (5) applied to
![]() . Using the abbreviation
. Using the abbreviation
![]()
![]() we also may write
we also may write
![]() . If
. If ![]() is set to
is set to ![]() , we obtain
, we obtain
since then
![]() . Therefore, in this case our quantum
symplectic bideterminants coincide with ordinary bideterminants which
are defined as products of minor
. Therefore, in this case our quantum
symplectic bideterminants coincide with ordinary bideterminants which
are defined as products of minor
![]() -determinants,
one factor for each entry
-determinants,
one factor for each entry
![]() of the composition
of the composition ![]() . According to familar notation
we write for a partition
. According to familar notation
we write for a partition ![]()
It should be remarked that the well known quantum determinants
corresponding to the general linear groups
(see for example [DD, 4.1.2, 4.1.7],
[CP, p. 236], [Tk, p. 152], [Ha1, p. 157])
can be defined in a similar
way using the quantum Yang-Baxter operator of type ![]() instead of our
instead of our
![]() . In contrast, explicit expressions for
quantum symplectic bideterminants become very complicated for
. In contrast, explicit expressions for
quantum symplectic bideterminants become very complicated for ![]() (apart from the case
(apart from the case
![]() in which case the
bideterminants
in which case the
bideterminants
![]() just are the monomials
just are the monomials
![]() ).
Denoting the fundamental weights
by
).
Denoting the fundamental weights
by
![]() one obtains a single
one obtains a single ![]() -minor determinant. If
-minor determinant. If ![]() , explicit
expressions are for example
, explicit
expressions are for example
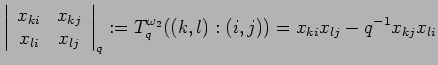
if
![]() and
and
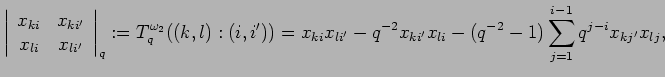
in the cases
![]() . The calculation of
. The calculation of
![]() for
for
![]() is really hard work. Note that such a bideterminant might be
different from
zero even if it contains two identical columns.
is really hard work. Note that such a bideterminant might be
different from
zero even if it contains two identical columns.