Details to the Proof of 11.3

We have to verrify the third equation listed in the proof. Let us first find suitable expressions for $\beta(c_i)$ and $\beta(d_i)$.

$$\begin{array}{rcl} \beta(c_i) & = & q^i\beta( v_{i'}v_{i})... ...= & -y^{-i} c_i+ (y-1)y^{-i}\sum_{k=1}^{i-1}c_k \end{array}$$

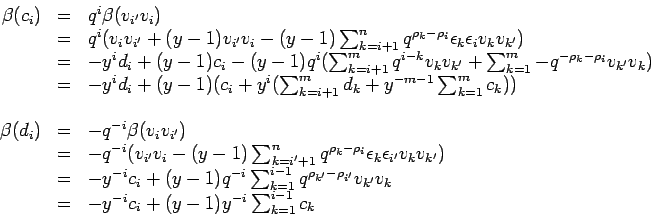
We obtain $\beta(y^{-i}c_i-y^{-1}d_i-(y^{-1}-1)\sum_{j=i+1}^md_j)=$

$$\begin{array}{rcl} & - & d_i+y^{-i}(y-1)c_i+(y-1)(\sum_{k=... ... -y^{-j}c_j + y^{-j}(y-1) \sum_{k=1}^{j-1} c_k ) \end{array}$$

Let us focus attention to the summand displayed in the last line:

$$\begin{array}{rcl} \sum_{j=i+1}^{m}( -y^{-j}c_j + y^{-j}(... ... (y-1) \sum_{j=i+1}^m\sum_{k=1}^{j-1} y^{-j}c_k \end{array}$$

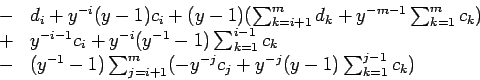
The second summand in this expression can be transformed in the following way:

$$\begin{array}{rcl} \sum_{j=i+1}^m\sum_{k=1}^{j-1} y^{-j}c_... ..._k + \sum_{k=i}^{m-1}(\sum_{j=k+1}^m y^{-j})c_k \end{array}$$

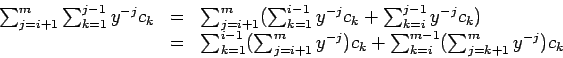
Thus:

$$\begin{array}{rcl} (y-1)\sum_{j=i+1}^m\sum_{k=1}^{j-1} y^{... ...m}\sum_{k=1}^{m} c_k +y^{-i}\sum_{k=i}^{i-1} c_k \end{array}$$

In order to get the last line you have to add $y^{-m}c_m -y^{-m}c_m$. Substituting this result into the above expression yields $\beta(y^{-i}c_i-y^{-1}d_i-(y^{-1}-1)\sum_{j=i+1}^md_j)=$

$$\begin{array}{rcl} & - & d_i+y^{-i+1}c_i-y^{-i}c_i+(y-1)\... ...\sum_{k=1}^{i-1} c_k - \sum_{k=i}^{m}y^{-k}c_k) \end{array}$$

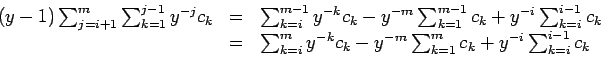
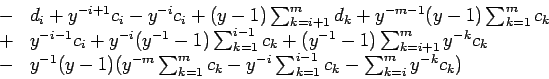
Now we see that almost all summands in this expression cancel each other an we end up with

$$\begin{array}{rcl} \beta(y^{-i}c_i-y^{-1}d_i-(y^{-1}-1)\su... ... & = & y^{-i+1}c_i-d_i +(y-1)\sum_{j=i+1}^md_j. \end{array}$$