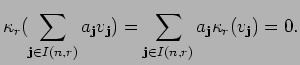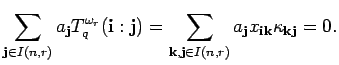We are going to prepare the proof of Proposition ![]() for general
for general ![]() . Since we need
a
. Since we need
a ![]() -analogue of [O2, Lemma 8.1], we have to investigate
the quantum symplectic exterior algebra.
We start with its definition
which can be found in many textbooks on
quantum groups (for instance [CP, chapter 7]).
It is defined as the quotient of the
tensor algebra
-analogue of [O2, Lemma 8.1], we have to investigate
the quantum symplectic exterior algebra.
We start with its definition
which can be found in many textbooks on
quantum groups (for instance [CP, chapter 7]).
It is defined as the quotient of the
tensor algebra
![]()
![]() by a certain ideal.
We denote it by
by a certain ideal.
We denote it by
![]() and write the symbol
and write the symbol
![]() for multiplication
in this algebra. Setting
for multiplication
in this algebra. Setting
for
![]() , we write down the defining relations holding in
, we write down the defining relations holding in
![]() according to [Ha2, (5.2)]:
according to [Ha2, (5.2)]:
where
![]() and
and
![]() is assumed. Remenber that the
is assumed. Remenber that the ![]() of
[Ha2] corresponds to the inverse of our
of
[Ha2] corresponds to the inverse of our ![]() .
The third relation does not occur in [Ha2] and indeed we have
.
The third relation does not occur in [Ha2] and indeed we have
PROOF: We use induction on ![]() . The beginning
. The beginning
![]() follows
directly from
follows
directly from
![]() by multiplication with
by multiplication with ![]() .
For
.
For ![]() we use (14) and the induction hypothesis to see that
we use (14) and the induction hypothesis to see that
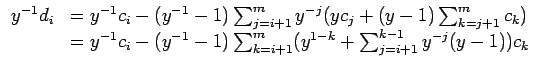
Since
![]() we obtain (15).
we obtain (15).
![]()
We set
In contrast to [O2, section 7] we take the usual
order ![]() on
on
![]() here for technical reasons. A subset
here for technical reasons. A subset
![]() ordered
in that way will be called an ordered subset in the sequel.
ordered
in that way will be called an ordered subset in the sequel.
PROOF: The fact that the set is a set
of ![]() -linear generators of
-linear generators of
![]() follows directly from the relations.
Linear independence is shown
using the Diamond Lemma for Ring Theory (cf. [Ha1, p. 157]).
The technical details can be found in Appendix 18.1.
follows directly from the relations.
Linear independence is shown
using the Diamond Lemma for Ring Theory (cf. [Ha1, p. 157]).
The technical details can be found in Appendix 18.1.
![]()
![]() is a graded algebra since the relations are
homogeneous of degree two. A basis for the
is a graded algebra since the relations are
homogeneous of degree two. A basis for the ![]() -th homogeneous summand
-th homogeneous summand
![]() is given by the subset
is given by the subset
![]() of
of
![]() corresponding to the
set
corresponding to the
set
![]() of subsets
of subsets
![]() having cardinality
having cardinality ![]() .
.
PROOF: It is a matter of calculation to show that
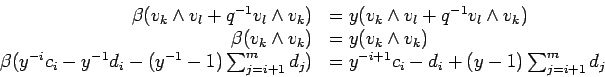
PROOF: By the previous proposition we have to show that the kernel of
![]() is an
is an
![]() subcomodul of
subcomodul of
![]() .
Call this kernel
.
Call this kernel ![]() and let
and let
![]() . We must show
. We must show
![]() . Since
. Since ![]() is a morphism of the
is a morphism of the ![]() -comodule
-comodule
![]() we see
we see
If ![]() is a bialgebra and
is a bialgebra and ![]() an algebra which is a
an algebra which is a ![]() -comodul we call
-comodul we call
![]() a
a ![]() -comodul algebra if multiplication as well as the embedding of the unit
element are morphisms of comodules.
-comodul algebra if multiplication as well as the embedding of the unit
element are morphisms of comodules.
PROOF: The tensor algebra
![]() over
over ![]() has a natural structure of an
has a natural structure of an
![]() -comolule algebra
(cf. [O1, 1.5]). Consequently by multiplicativity and the above proposition
the ideal generated by the kernel of
-comolule algebra
(cf. [O1, 1.5]). Consequently by multiplicativity and the above proposition
the ideal generated by the kernel of
![]() is an
is an
![]() -comodule. But this is precisely the defining ideal
of
-comodule. But this is precisely the defining ideal
of
![]() by Proposition 11.3. Thus
by Proposition 11.3. Thus
![]() inherits
the comodul algebra structure from
inherits
the comodul algebra structure from
![]() .
.
![]()
Denote the comodule structure map of
![]() by
by
![]()
![]() .
.
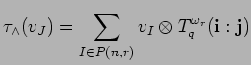
where
![]() and
and
![]() are the multi-indices corresponding to the
ordered subsets
are the multi-indices corresponding to the
ordered subsets
![]() and
and
![]() ,
respectively.
,
respectively.
Let us first treat the ingredients needed in the proof of that proposition.
PROOF: Since the
defining ideal of
![]() is generated by the kernel of
is generated by the kernel of
![]() by Proposition 11.3
the assertion immediately follows
from Lemma 9.1.
by Proposition 11.3
the assertion immediately follows
from Lemma 9.1.
![]()
Let
![]()
![]() be the
set of multi-indices corresponding to the ordered subsets
be the
set of multi-indices corresponding to the ordered subsets
![]() .
.
PROOF: We use induction on ![]() . The case
. The case ![]() directly follows
from the formulas
directly follows
from the formulas
which are valid for
![]() and
and ![]() .
If
.
If ![]() , we embed
, we embed
![]() as the subgroup of
as the subgroup of
![]() that
fixes the letter
that
fixes the letter ![]() .
If
.
If
![]() , there is nothing to prove since
, there is nothing to prove since
![]() . Otherwise, we may write
. Otherwise, we may write
![]() where
where
![]() and
and
![]() .
.
First consider the case where
![]() is not contained in
is not contained in
![]() .
Applying
.
Applying
![]() to
to
![]() we only have to use (17) but not
(18). Consequently, we have
we only have to use (17) but not
(18). Consequently, we have
![]() .
Here,
.
Here,
![]() denotes the omission of
denotes the omission of ![]() . This element obviously
lies in
. This element obviously
lies in ![]() , proving the assertion in the case
, proving the assertion in the case
![]() .
If
.
If ![]() is not the identity map we have
is not the identity map we have
![]() by the induction hypothesis since
by the induction hypothesis since
![]() .
.
We next consider the case
![]() .
This forces
.
This forces ![]() because
because ![]() . Let
. Let ![]() .
As above, we have
.
As above, we have
![]() . Applying
. Applying
![]() to this expression, we have to use
(18) for the first time. But for each
basis element
to this expression, we have to use
(18) for the first time. But for each
basis element
![]() occurring as a summand in the resulting
expression we have
occurring as a summand in the resulting
expression we have
![]() .
Similar things happen concerning the remaining
.
Similar things happen concerning the remaining
![]() . Thus, for each
. Thus, for each
![]() occurring
as a summand in
occurring
as a summand in
![]() ,
it follows
,
it follows
![]() . On the other hand, for each such
summand there must exist an
. On the other hand, for each such
summand there must exist an ![]() where
where ![]() . This is because
. This is because ![]() must contain a pair
must contain a pair ![]() for some
for some
![]() , since this was the
case for the multi-index
, since this was the
case for the multi-index ![]() we started with and
we started with and ![]() either exchanges
the position of such a pair or replaces it by a sum where other such pairs
occur in each summand. Consequently,
we obtain
either exchanges
the position of such a pair or replaces it by a sum where other such pairs
occur in each summand. Consequently,
we obtain
![]() in this case too.
in this case too.
![]()
Let the coefficient matrices of the ![]() -module homomorphisms
-module homomorphisms
![]() and
and ![]() (from Lemma 11.7)
be given by
(from Lemma 11.7)
be given by
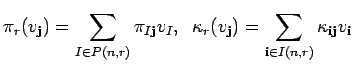 and
and 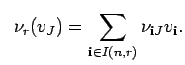
Now, if
![]() corresponds to the
ordered set
corresponds to the
ordered set
![]() we have
we have
![]() yielding
yielding
![]() by Lemma 11.7. From Lemma
11.8 it follows
by Lemma 11.7. From Lemma
11.8 it follows
![]() modulo
modulo ![]() . Thus, for a pair
. Thus, for a pair
![]() of multi-indices corresponding to ordered sets
of multi-indices corresponding to ordered sets
![]() , we obtain
, we obtain
![]() (Kronecker symbol). Finally, from
(Kronecker symbol). Finally, from
![]() we see for all
we see for all
![]() and
and
![]()
We are now ready to give the proof of proposition 11.6. We calculate
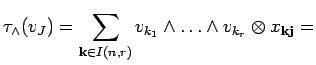
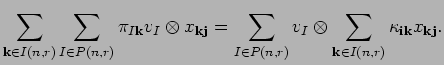
But, this is exactly what we wanted
by
the definition
![]() of bideterminants.
of bideterminants.
The formula we just have proved has some useful consequences
concerning the comultiplication and augmentation of
![]() . These
are valid for any pair
. These
are valid for any pair
![]() of multi-indices corresponding to ordered sets
of multi-indices corresponding to ordered sets
![]() and
follow directly with the help of the comodule axioms
and
follow directly with the help of the comodule axioms
![]() and
and
![]() :
:
Another useful consequence is the following corollary:
PROOF: By Lemma 11.7 and the assumption we have