The Symplectic
Remember that
![]() is a coalgebra for each
is a coalgebra for each
![]() . Therefore, its dual
. Therefore, its dual ![]() -module inherits the structure of an
-module inherits the structure of an
![]() -algebra. We define
-algebra. We define
and call it the symplectic ![]() -Schur algebra. Two linear forms
-Schur algebra. Two linear forms
![]() are multiplied by convolution, that is
are multiplied by convolution, that is
for all
![]() . The reader may verify that
one obtains the symplectic Schur algebra in the classical situation
as defined in [O2]. This also is identical to the symplectic
Schur algebra in the sense of S. Donkin, respectively S. Doty
([Do2] respectively [Dt]).
One aim is to show that the construction
is stable under base changes and that it is a free
. The reader may verify that
one obtains the symplectic Schur algebra in the classical situation
as defined in [O2]. This also is identical to the symplectic
Schur algebra in the sense of S. Donkin, respectively S. Doty
([Do2] respectively [Dt]).
One aim is to show that the construction
is stable under base changes and that it is a free ![]() -module.
Both facts follow when we have shown that
-module.
Both facts follow when we have shown that
![]() is free as
an
is free as
an ![]() -module. Further
we want to initiate the study of the representation theory of this algebra.
An easy way to do this is to
check that the axioms of a cellular algebra given by J. Graham
and G. Lehrer in [GL] hold. These axioms
are as follows:
-module. Further
we want to initiate the study of the representation theory of this algebra.
An easy way to do this is to
check that the axioms of a cellular algebra given by J. Graham
and G. Lehrer in [GL] hold. These axioms
are as follows:
Let ![]() be an associative unital algebra over a commutative unital ring
be an associative unital algebra over a commutative unital ring ![]() together with a partially ordered finite set
together with a partially ordered finite set
![]() and finite sets
and finite sets
![]() to each
to each
![]() (the
set of
``
(the
set of
``![]() -tableaux'').
-tableaux''). ![]() is called a cellular algebra if the following
properties hold:
is called a cellular algebra if the following
properties hold:
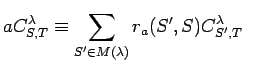 mod
mod
holds, where the elements
![]() are independent of
are independent of ![]() and
and
![]() is defined as the
is defined as the ![]() -linear span of basis elements
-linear span of basis elements
![]() where
where
![]() and
and
![]() .
.
Starting with these axioms the representation theory of ![]() is developed in
[GL] along the following lines. To each
is developed in
[GL] along the following lines. To each
![]() a standard module
a standard module
![]() is defined on a
free
is defined on a
free ![]() -basis
-basis
![]() .
An element
.
An element ![]() acts on it via
acts on it via
![]() .
Each
.
Each
![]() possesses a symmetric
bilinear form
possesses a symmetric
bilinear form
![]() for which the formula
for which the formula
![]() is valid
for all
is valid
for all ![]() and
and
![]() . In the case where
. In the case where ![]() is a field
and
is a field
and
![]() ,
the radical of
,
the radical of
![]() is the same as the radical of the bilinear form
is the same as the radical of the bilinear form
![]() . The simple head
. The simple head
![]() of
of
![]() then is absolutely
irreducible. In this way a complete set of pairwise non-isomorphic
simple
then is absolutely
irreducible. In this way a complete set of pairwise non-isomorphic
simple ![]() -modules
-modules
![]() can be
obtained. Here we have set
can be
obtained. Here we have set
![]() .
.
Denoting the multiplicity of ![]() in
in
![]() by
by
![]() to
each
to
each
![]() and
and
![]() Graham and Lehrer show that
Graham and Lehrer show that
![]() for
for
![]() and
and
![]() . To each order refining the given partial order on
. To each order refining the given partial order on
![]() the corresponding decomposition matrix
the corresponding decomposition matrix
![]() is unitriangular.
The Cartan-matrix
is unitriangular.
The Cartan-matrix ![]() can be calculated as
can be calculated as
![]() . The theory also supplies a criterion to decide whether
. The theory also supplies a criterion to decide whether ![]() is
semisimple or quasi-hereditary. In the first case we must have
is
semisimple or quasi-hereditary. In the first case we must have
![]() for all
for all
![]() whereas in the
second case
whereas in the
second case
![]() will do.
will do.
Examples of cellular algebras are the Brauer centralizer algebras
![]() ,
Ariki-Koike-Hecke-algebras, Temperley-Lieb and Jones algebras ([GL]).
R.M. Green ([GR]) constructs a
,
Ariki-Koike-Hecke-algebras, Temperley-Lieb and Jones algebras ([GL]).
R.M. Green ([GR]) constructs a ![]() -analogue of the
codeterminant basis (in the sense of [Gr])
for the classical Schur algebra
-analogue of the
codeterminant basis (in the sense of [Gr])
for the classical Schur algebra
![]() which is cellular as well.
The corresponding standard modules
which is cellular as well.
The corresponding standard modules
![]() are precisely the
are precisely the
![]() -Weyl modules in the sense of [DJ2] (see [GR],
Proposition 5.3.6).
-Weyl modules in the sense of [DJ2] (see [GR],
Proposition 5.3.6).
It should be remarked that the finiteness of ![]() is not postulated in the
original definition. Since this property is valid in our example we impose this
restriction to avoid unnecessary trouble (cf. discussion in [KX],
section 3).
is not postulated in the
original definition. Since this property is valid in our example we impose this
restriction to avoid unnecessary trouble (cf. discussion in [KX],
section 3).
Since we have defined the symplectic ![]() -Schur algebra as the dual module
of a coalgebra we now translate the concept of cellular algebras
to coalgebras:
-Schur algebra as the dual module
of a coalgebra we now translate the concept of cellular algebras
to coalgebras:
Let ![]() be a coalgebra over a commutative unital ring
be a coalgebra over a commutative unital ring ![]() ,
together with a partially ordered finite set
,
together with a partially ordered finite set
![]() and finite
sets
and finite
sets
![]() for each
for each
![]() .
We call
.
We call ![]() a cellular coalgebra
if the following properties hold:
a cellular coalgebra
if the following properties hold:
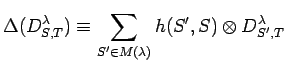 mod
mod
holds, where the coalgebra elements
![]() are independent of
are independent of ![]() and
and
![]() is defined as the
is defined as the
![]() -linear span of basis elements
-linear span of basis elements
![]() where
where
![]() and
and
![]() .
.
To an arbitrary ![]() -coalgebra the dual algebra is well defined. The dual
coalgebra of an algebra
-coalgebra the dual algebra is well defined. The dual
coalgebra of an algebra ![]() is well defined if the algebra is known to be
projective as an
is well defined if the algebra is known to be
projective as an ![]() -module, since then
-module, since then
![]() .
In the case of a cellular algebra this is
obviously valid. The connection between the above two concepts is given by
the following proposition which can be proved straightforwardly using
structure constants with respect to the bases (cf. [O1, 4.2.3]).
.
In the case of a cellular algebra this is
obviously valid. The connection between the above two concepts is given by
the following proposition which can be proved straightforwardly using
structure constants with respect to the bases (cf. [O1, 4.2.3]).
According to the proposition our next task is to find a cellular basis
for the coalgebra
![]() together with an appropriate involution map
such that the axioms of the cellular coalgebra hold. As soon as this is done
the representation theory of
together with an appropriate involution map
such that the axioms of the cellular coalgebra hold. As soon as this is done
the representation theory of
![]() is developed to the extent
indicated above.
is developed to the extent
indicated above.