In the definition of the symplectic monoid
![]() we have introduced a
function called the coefficient of dilation. This is neccessarily
a regular function in the sense of algebraic geometry.
Now we will define its quantization which will be
called the quantum coefficient of dilation.
Using
notation (2) we see that
we have introduced a
function called the coefficient of dilation. This is neccessarily
a regular function in the sense of algebraic geometry.
Now we will define its quantization which will be
called the quantum coefficient of dilation.
Using
notation (2) we see that
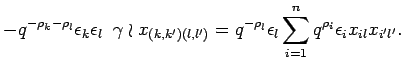
is independent of ![]() , whereas
, whereas
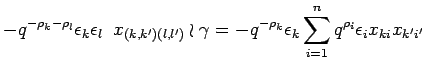
is independent of ![]() . But, as
. But, as
![]() according to (5),
both expressions coincide and consequently are independent of both
according to (5),
both expressions coincide and consequently are independent of both
![]() and
and ![]() . Thus, the element
. Thus, the element
is well defined in
![]() . In fact it is a grouplike element of
this bialgebra. More precisely it is the coefficient function of the
one dimensional subcomodule of
. In fact it is a grouplike element of
this bialgebra. More precisely it is the coefficient function of the
one dimensional subcomodule of
![]() that is spanned by the
tensor
that is spanned by the
tensor
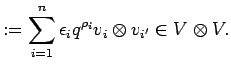
To see this, note that
![]() for each
for each ![]() and that
and that ![]() is a morphism of
is a morphism of
![]() -comodules. One calculates
-comodules. One calculates
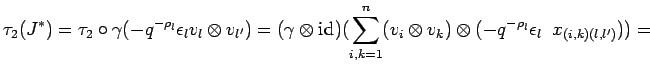
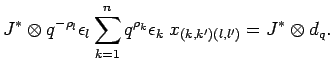
PROOF: We calculate
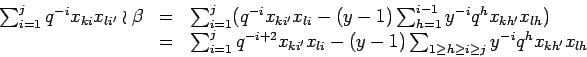
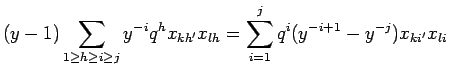
For ![]() we deduce the connection formula
we deduce the connection formula
PROOF: By definition of bideterminants and the above lemma we have
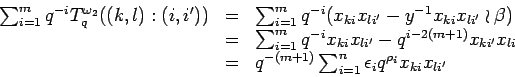
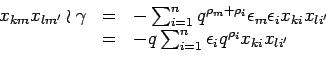
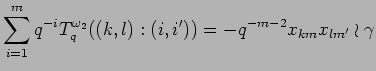
Since
![]() it follows that the expression vanishes if
it follows that the expression vanishes if ![]() . In the case
. In the case
![]() we deduce from (7) the equation
we deduce from (7) the equation
![]() which finishes the proof.
which finishes the proof.
![]()