As examples we will treat the ![]() -group algebras
-group algebras ![]() of symmetric groups.
Here the standard modules
of symmetric groups.
Here the standard modules ![]() are known to be the
Specht modules ([GL], 5.7,
see [JK], chapter 7 for details on Specht-modules). The reader
not familiar with cellular algebras may check imediately that the
conditions stated in the begining of section 5
can be realised using this modules.
They are labelled by the set
are known to be the
Specht modules ([GL], 5.7,
see [JK], chapter 7 for details on Specht-modules). The reader
not familiar with cellular algebras may check imediately that the
conditions stated in the begining of section 5
can be realised using this modules.
They are labelled by the set
![]() of partitions of n and are defined as
submodules of permutation modules
of partitions of n and are defined as
submodules of permutation modules ![]() on the cosets of parabolic
subgroups corresponding to the partition
on the cosets of parabolic
subgroups corresponding to the partition ![]() .
As first example, let us look at
.
As first example, let us look at ![]() .
Then
.
Then ![]() is the permutation representation on the cosets of the copy of
is the permutation representation on the cosets of the copy of ![]() in
in
![]() fixing the last element n. As a
fixing the last element n. As a ![]() -module this is free
of rank n with basis
-module this is free
of rank n with basis ![]() , say. The operation of
, say. The operation of
![]() from the right is given by
from the right is given by ![]() .
The Specht module
.
The Specht module ![]() is the free
is the free ![]() -submodule with
basis
-submodule with
basis ![]() for
for ![]() .
.
The symmetric bilinear form ![]() is
given by restriction of the canonical bilinear form on
is
given by restriction of the canonical bilinear form on ![]() (given by the unit matrix) to
(given by the unit matrix) to ![]() . Thus the Gram matrix
of
. Thus the Gram matrix
of ![]() is nothing but the Cartan matrix
corresponding to the Dynkin diagram of type
is nothing but the Cartan matrix
corresponding to the Dynkin diagram of type ![]() .
This in turn is just the coefficient matrix of
.
This in turn is just the coefficient matrix of
![]() with respect to the basis
with respect to the basis ![]() on
on ![]() and the corresponding dual basis
and the corresponding dual basis ![]() on
on
![]() . The image of
. The image of ![]() is consequently
the span of the columns of this matrix and is easily calculated to be
the span of
is consequently
the span of the columns of this matrix and is easily calculated to be
the span of ![]() and
and ![]() for
for ![]() . Therefore
. Therefore ![]() - the cokernel of
- the cokernel of ![]() - is generated
by
- is generated
by ![]() and is obviously isomorphic to
and is obviously isomorphic to ![]() as a
as a ![]() -module.
-module.
Let us show that the operation of ![]() on
on ![]() is
trivial. We only need to check this for the long cycle
is
trivial. We only need to check this for the long cycle ![]() or its inverse and
or its inverse and ![]() .
On
.
On ![]() the operation
is given by
the operation
is given by
![]() and
and ![]() for i>1
in the case of
for i>1
in the case of ![]() whereas we have
whereas we have ![]() and
and ![]() for all i>2. Transposing the
corresponding coefficient matrices we get
for all i>2. Transposing the
corresponding coefficient matrices we get ![]() . Since
. Since ![]() is congruent to
is congruent to ![]() modulo
the image of
modulo
the image of ![]() we are done.
we are done.
The Specht module of the partition ![]() is just the one-dimensional
trivial representation with bilinear form
is just the one-dimensional
trivial representation with bilinear form ![]() being
given by the trivial Gram matrix. Therefore
being
given by the trivial Gram matrix. Therefore
![]() holds in
holds in
![]() . Moreover, we have shown the following equation in
. Moreover, we have shown the following equation in
![]() :
:
![]()
In the case of the
symmetric group ![]() there are three partitions
there are three partitions
![]() and
and ![]() . The
corresponding Specht modules are free
. The
corresponding Specht modules are free ![]() -modules
of rank 1, 2 and 1, respectively. The cases
-modules
of rank 1, 2 and 1, respectively. The cases ![]() and
and
![]() have been treated in general above. The Specht module
have been treated in general above. The Specht module
![]() is the sign representation and
is the sign representation and ![]() . Therefore we have
. Therefore we have ![]() . From the ordinary decomposition matrices
of
. From the ordinary decomposition matrices
of ![]() for the primes 2 and 3 we get
for the primes 2 and 3 we get
![]() and
and
![]() leading to the
global decomposition matrix of
leading to the
global decomposition matrix of ![]() :
:

Note that the corresponding equations according to condition (c)
of Proposition 5.6 even hold in ![]() . This will not
be true in the next example
. This will not
be true in the next example ![]() as well as the fact that the
global decomposition matrix can entirely be constructed from
the knowledge of the ordinary decomposition matrices for the primes
2 and 3. On the other hand, the
ordinary decomposition numbers are detected from the
above by multiplying the whole table by [2] resp. [3] and then
setting [2]=1 resp. [3]=1.
as well as the fact that the
global decomposition matrix can entirely be constructed from
the knowledge of the ordinary decomposition matrices for the primes
2 and 3. On the other hand, the
ordinary decomposition numbers are detected from the
above by multiplying the whole table by [2] resp. [3] and then
setting [2]=1 resp. [3]=1.
Before proceeding to the next example let us write down all the
relations between the ![]() with the help of
Proposition 5.8.
We have to consider two pairs
with the help of
Proposition 5.8.
We have to consider two pairs ![]() such that
such that ![]() . These are
. These are ![]() and
and ![]() . We calculate
. We calculate
![]() and
and
![]() . This gives
. This gives
![]() and
and
![]() leading to the following complete set of relations for
leading to the following complete set of relations for ![]() and
and
![]() :
:
![]()
Turning to ![]() we have 5 partitions
we have 5 partitions
![]() and
and ![]() . Let us first picture
the global decomposition matrix and then comment it:
. Let us first picture
the global decomposition matrix and then comment it:
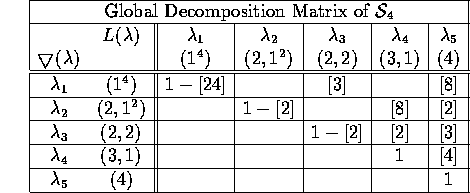
First note that the entries [8] and [4] cannot be reconstructed from
the knowledge of the ordinary decomposition matrices of ![]() .
As in the preceeding example the first row follows easily
from
.
As in the preceeding example the first row follows easily
from ![]() and the knowledge
of
and the knowledge
of ![]() and
and
![]() . Note that
. Note that
![]() does not hold in
does not hold in
![]() but surely in
but surely in ![]() .
In contrast, the equations corresponding to
the rows 3,4,5 hold in
.
In contrast, the equations corresponding to
the rows 3,4,5 hold in ![]() the last two of which have
been treated in the beginning of this chapter.
We leave the calculation of
the last two of which have
been treated in the beginning of this chapter.
We leave the calculation of ![]() as an exercise and turn to the
most interesting case
as an exercise and turn to the
most interesting case ![]() .
.
Here the Specht module is a free ![]() -module of rank three with basis
-module of rank three with basis
![]() , say. The long cycle
, say. The long cycle ![]() and
and ![]() operate from right by
operate from right by ![]() and
and ![]() . The
Gram matrix of the bilinear form is given by
. The
Gram matrix of the bilinear form is given by
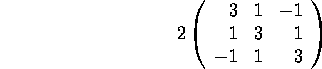
and therefore the image of ![]() is spanned by
is spanned by ![]() and
and ![]() . Clearly,
. Clearly, ![]() is isomorphic
to [8]+[8]+[2] as a
is isomorphic
to [8]+[8]+[2] as a ![]() -module. But anyway, as an A-module
it is irreducible by
-module. But anyway, as an A-module
it is irreducible by ![]() -sums as defined in chapter 2. Therefore it cannot be splitted in
-sums as defined in chapter 2. Therefore it cannot be splitted in ![]() anymore.
But we can calculate in
anymore.
But we can calculate in ![]() as in the proof of Lemma
5.1. From the ordinary decomposition matrix for the
prime 2, we get
as in the proof of Lemma
5.1. From the ordinary decomposition matrix for the
prime 2, we get
![]() and by dimension arguments the 2-residual series must be
and by dimension arguments the 2-residual series must be
![]()
which completes the verification. In order to determine the relations
among the ![]() one calculates
one calculates
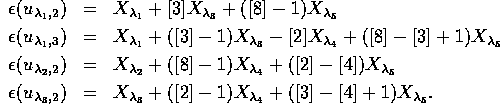
As in the case of ![]() a complete set of relations can be
obtained from these formulas with help of Proposition 5.8.
a complete set of relations can be
obtained from these formulas with help of Proposition 5.8.
Problems: