We now restrict A to a special type of R-algebra which have been
described using a couple of axioms by Graham and Lehrer
([GL]) and which are called cellular algebras.
Instead of listing these axioms we rather explain the properties
of A and 
which will be needed in the sequel. For more details we refer to
[GL].
and for each 
a pair 
of A-modules called the standard and the costandard
module of type 
. Both are free and isomorphic to each other as
R-modules and there is an A-module homomorphism
is again a cellular algebra and the
functor 
carries 
to the corresponding objects and
morphisms 
with respect to 
.
of
is an irreducible 
-module
as long as is not the zero map. All
irreducible -modules occur in this way. Furthermore, if
and 
, then
the (nesessarily absolutely) irreducible modules and
are non isomorphic.
such that 
,
let 
be the multiplictiy of as a
composition factor of 
. Then 
and
implies 
.
Let us compare these statements with corresponding definitions and results in
[GL]. We assume that A is finitely generated as
an R-module. This implies the finiteness of .
Now, as we consider right modules, our 
corresponds to
in [GL]. The costandard modules are defined
as their duals
where the action of A is given by 
for all 
and 
.
Here * denotes the anti involution on A which exists by one of
the axioms. Now, on 
there is a symmetric bilinear form
with 
.
Since coincides with as an R-module
we have a bilinear form on
with 
(since the
operation on is just the left action on
pulled to the right via *).
This in turn leads to the A-module homomorphism 
being defined by 
.
The compatibility
with the functor 
is obvious (compare (1.8) in [GL]).
The statements concerning the follow from
(3.2) and (3.4) of [GL]. For this purpose, note that the
radical of is nothing but the kernel of
where again the action of A is pulled from left to right via *.
Finally, the statement on the decomposition numbers
follows from (3.6) of [GL].
If K is a field and all are isomorphisms, then
according to Theorem (3.8) of [GL] is semisimple.
For the field Q of fractions on an integral domain
R this is by flatness the case
iff is injective for all .
If this is the case call A generic semisimple. Even for such
an A it is possible that 
for some field K.
For a prime p we will throughout denote by F:=[p]=R/(p) the
corresponding residue class field for short. We set
According to (3.10) in [GL] for a field K, the algebra
is quasi-hereditary if 
for all . Let us call A integrally quasi-hereditary if
for all primes 
.
We now define a global version of in 
.
Throughout, we will not distinguish between right A-modules and
their residue classes in 
or 
any more. Let 
be
the cokernel of . We set
Note that 
is not the residue class
of some A-module in general. But if K is a field and an
R-algebra, then the map 
of chapter 3 carries this element to the
residue class of in the Grothendieck group
.
Let 
be the
-linear span of all in
.
We wish to show that for a generic semisimple cellular algebra A over
a pid you always have 
. From now on, let us assume
that R is a pid. We call an element 
positive
if in the unique expression with respect to the 
-basis
of all integer coefficients are
nonnegative. Write 
for the submonoid of
all these elements and
for the span of 
in . Note that 
is zero,
iff [p]x=0 for all primes p, whereas 
is zero,
iff the residual series 
in is zero for all primes p.
PROOF:Since the R-annihilator of 
is contained in the R-annihilator
of xa for all 
, it follows that the R-module
decomposition of M into primary components is in fact a
decomposition of A-modules. Thus we may assume that M is
primary as an R-module. Let p be the corresponding prime.
Now for all primes 
the residual series 
is constant zero. Let us consider 
. Recall that F:=R/(p)
and 
means
, that is
. Since these
simple 
-modules form a basis of the Grothendieck group of ,
there are unique nonnegative integers 
such that
For all
there is an -epimorphism
given by multiplication by p. This shows that
is nonnegative. There is a smallest
number j, such that 
for all 
,
since M is a torsion module.
We set
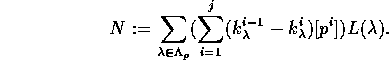
This is obviously contained in . By Lemma 4.1
it remains to show that 
for all primes q.
For both series are identically zero. For q=p
by multiplicativity of 
, it is enough to show
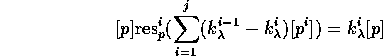
for all i. This can be calculated with help of (3).
PROOF:This is immediate from the definition of and the
Lemma 5.1 since under the above assumption
is an R-torsion module.
PROOF:By Lemma 4.1
we have to show that the residual series of M and N
coincide for all primes p. The epimorphism from
to 
considered in the proof
of Lemma 5.1 and being induced by multiplication by p
must be an isomorphism in the case of a free module. Therefore,
the residual series of M and N are constant.
Thus the proof is finished as soon as
we have shown [p]M=[p]N for all primes p.
Since the sum M+N
in V again is a full lattice,we can
reduce to the case 
.
Now let 
be the localisation of R
at the prime ideal (p) and 
,
the corresponding lattices in V.
Multiplication by [p] - the residue class in 
of the field 
-
is defined in 
as well and leads to the same
elements [p]M'=[p]M resp. [p]N'=[p]N in the Grothendieck group
(see Propositions 3.1 and 3.2).
Finishing the proof now is standard (cf. [CR], 16.16).
Applying Lemma 5.3 to the image of and
as lattices in 
, one immediately
gets
PROOF:By Lemma 5.1 we can reduce to the case where
M is free as an R-module, since an arbitrary M can be written
with 
free and 
an R-torsion module (even in
). Let Q be the field of fractions on R. Since A is
generic semisimple, 
decomposes into a direct
sum of simple modules 
.
Let 
be the direct sum of the corresponding
. Both M and N are full lattices in 
so that it follows M=N in by Lemma 5.3.
Since 
by Corollary 5.2 the proof is
finished.
Throughout, let us now assume that A is generic semisimple.
Note that in this case the set 
defined above is finite
for all .
Set 
where 
is the largest number such that 
.
PROOF:To show existence, there are elements 
such that 
by Lemma 5.1. Furthermore, the proof of this
lemma shows that 
for all 
. If we multiply the equation
by [p].
Because 
and 
, we get
thus
.
Because 
, this in
turn implies 
for all .
Setting 
and
for
we are finished since
and obviously 
.
For uniqueness, take 
to be a second set of such
elements. Since 
by
definition and for both elemens are in ,
it is enough to show
for all primes p.
In the case this follows from condition (b). Using (b) and multiplying (c)
by [p] we get from Proposition 3.2
for all 
where 
are the
usual decomposition numbers for . To this claim, note that
in by Corollary 5.4 and
Proposition 3.2.
This completes the proof.
For any field K you have 
where
is the map induced
by the base change to K (see chapter 3).
Therefore, we call these elements the global decomposition
numbers of A.
PROOF:Since 
there must be a prime
such that 
. This implies
for the residue class field F=R/(p).
The corresponding known result for fields then implies the statement
of the proposition.
For any total order on refining the given partial
order, the matrix 
is therefore upper triangular with respect to this total order.
Setting 
and
for one gets a
unitriangular (and so invertible) matrix
.
Note that condition (c) of
proposition 5.6 holds for the 
, too.
We call D the global decomposition matrix and E the
regular decomposition matrix. The fact that E is invertible
implies that is generated as an module by the
costandard modules , too.
Let us determine the relations among the resp. the
. Denote by 
the canonical
basis elements of the free -module 
.
We define two epimorphisms
by 
and 
. If 
is the
automorphism of given by the regular
decomposition matrix E, i.e. 
, we clearly have 
. Let 
and 
be the kernels of 
and
respectively. We only need to determine since
.
Let be a prime such that 
. Since
for all we have 
the costandard modules 
form a basis of the Grothendieck group . Therefore
there are unique integers 
for all 
and such that
For each pair 
with we set
and let 
be the -linear span of all elements
for such pairs and positive
integers .
PROOF:Since the residual series of the costandard modules are constant we have for a prime q
Now, 
whenever by the formulas
(1) and (3). Multiplying the bracket term by
[p] gives zero by construction of the numbers
. Therefore 
for all primes q, thus 
.
Now let 
be in with 
. We first claim
that there exists 
such that 
for all 
and primes .
For if there is 
and a prime such
that for all there exists 
giving
, it follows that the coefficient
of 1 in the unique presentation of 
with respect
to the -basis of is nonzero.
Now, if Q is the field of fractions on R and 
the corresponding map of chapter
3 we must have 
. But this implies
since all costandard modules form a basis of 
. This
contradict 
in .
We now proceed by induction on such a number i.
For i=0 we must have x=0 since then the residual series
of all 
are zero for all primes. Assume i>0.
There are uniquely determined numbers 
such that
. Set
Then 
. Write 
. By construction of y we have
for all
and all primes p.
We claim 
for all primes p and
. If this is shown the induction hypothesis
applies to z giving 
as required.
Keep p fixed and let
. The coefficient of in y
is of the form 
with some 
being nonzero only for a finite number
of primes q. Since 
, it
follows 
by definition of 
. Making use of
we calculate
where in addition we used the fact that the residual series of
is constant. Since 
is a basis of the coefficients
must be zero for as well.
Clearly 
iff A is integrally quasi-hereditary. Thus we
have proved
Examples of integrally quasi-hereditary generic semisimple cellular algebras are given by Schur algebras and generalizations of them.
