Centralizer Coalgebras

Let $R$ be a noetherian integral domain, $V$ a free $R$-module with a fixed basis $\{v_{1}, \ldots , v_{n}\}$. Let $e_{i}^{ j}$ denote the corresponding basis of matrix units for ${\cal E}:={\rm End}_{R}{(V)}$. The algebra structure on ${\cal E}$ induces a coalgebra structure on the dual $R$-module ${{\cal E}}^*:={\rm Hom}_{R}{({\cal E},R)}$. On the dual basis elements the comultiplication $\Delta$ and the counit $\epsilon$ are given by

$$\Delta ({{e}^*_{i}}^{j})=\sum_{k=1}^n {{e}^*_{i}}^{k} \otimes {{e}^*_{k}}^{j} ,\; \; \epsilon ({{e}^*_{i}}^{j}) =\delta_{ij}.$$

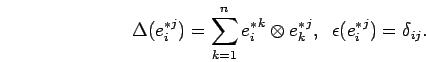
We will be engaged with epimorphic coalgebra images of ${{\cal E}}^*$ since they correspond to subalgebras of ${\cal E}$. Consider the isomorphism ${\vartheta}_{tr}:{\cal E}\rightarrow {{\cal E}}^*$ of $R$-modules induced by the nondegenerate bilinear form corresponding to the matrix trace map $tr:{\cal E}\rightarrow R$, i.e. ${\vartheta}_{tr}(\mu)(\nu):= tr(\mu\nu)$. Note that ${\vartheta}_{tr}$ maps $e_{i}^{ j}$ onto ${{e}^*_{j}}^{i}$. Let $A\subseteq {\cal E}$ be an arbitrary subset and $L(A)$ the $R$-linear span in ${\cal E}$ of all commutators $[\nu, \mu ]=\nu\mu-\mu\nu$ where $\nu$ runs through $A$ and $\mu$ runs through ${\cal E}$. We set $K(A):={\vartheta}_{tr}(L(A))\subseteq {{\cal E}}^*$. If $A$ consists of just one element $\nu$ we use abbreviations $L(\nu)$ and $K(\nu)$ for $L(A)$ and $K(A)$.

Lemma 2.1   $K(A)$ is a coideal in ${{\cal E}}^*$ for each subset $A\subseteq {\cal E}$.

SKETCH OF PROOF: Since the sum of coideals is a coideal again we only need to consider the case $A=\{\nu\}$. Using an explicit expression for $\nu$ in terms of the basiselements $e_{i}^{ j}$ one calculates for arbitrary numbers $k,l \in \{1,\ldots, n\}$:

$$\Delta ({\vartheta}_{tr}([\nu ,e_{k}^{ l}]))= \sum_m ( {{e}^*... ...artheta}_{tr}([\nu, {{e}^*_{m}}^{l}]) \otimes {{e}^*_{m}}^{k},$$

which just means

$$\Delta (K(\nu)) \subseteq K(\nu) \otimes {{\cal E}}^*+ {{\cal E}}^* \otimes K(\nu).$$

In a simialar way one shows $\epsilon (K(\nu))=0$. A more detailed proof can be found in section 1.3 of [Oe].$\Box$

If $C$ is an arbitrary coalgebra such that $V$ is a $C$-comodule with structure map $\tau_{V}:V\rightarrow V\otimes C$ we denote the set of $C$-comodule endomorphisms by

$${\rm End}_{C}{(V)}:=\{ \mu \in {\cal E}\vert\; \; (\mu \otimes {\rm id}_{C}) \circ \tau_{V}= \tau_{V} \circ \mu \}.$$

Clearly this is a subalgebra of ${\cal E}$. The proof of the next lemma is similar to the preceeding one.

Lemma 2.2   Let $C$ be a coalgebra together with an epimorphism $\pi: {{\cal E}}^*\rightarrow C$. Then

$$\mu \in {\rm End}_{C}{(V)} \Longleftrightarrow K(\mu) \subseteq {\rm ker}(\pi).$$

Corollary 2.3   Let $M$ be a coideal in ${{\cal E}}^*$ and $\mu , \nu \in {\cal E}$. Then $K(\mu) \subseteq M$ and $K(\nu) \subseteq M$ implies $K(\mu \nu) \subseteq M$ and $K(\nu\mu ) \subseteq M$.

We now define the centralizer coalgebra of the subset $A\subseteq {\cal E}$ as

$$M(A):={{\cal E}}^*/ K(A).$$

According to lemma 2.2 we have

$$A \subseteq {\rm End}_{M(A)}{(V)}.$$

Furthermore $M(A)$ is the largest epimorphic image of ${{\cal E}}^*$ with this property. By the corollary $M(A)$ does not change if $A$ is substituted by its algebraic span. Before going deeper into the analysis of relationships between $M(A)$ and the centralizer algebra

$$C(A):={\rm End}_{A}{(V)}=\{ \mu \in {\cal E}\vert\; [\mu , \nu]=0, \;\mbox{ for all } \nu \in A\}$$

we give a presentation of $M(A)$ by generators and relations, which is convenient for practical use.

The residue classes of the basis elements ${{e}^*_{i}}^{j}$ with respect to any coideal in ${{\cal E}}^*$ will always be denoted by $x_{i j}$ where $i,j\in \underline{n}:=\{1, \ldots , n\}$. If $\mu =\sum_{i,j=1}^n a_{ij}e_{i}^{ j}\in {\cal E}$ is arbitrary we write

$$\mu x_{i j} :=\sum_{k=1}^n a_{ik}x_{kj \}; \; \mbox{ and } \; \; x_{i j}\mu :=\sum_{k=1}^n x_{i k}a_{kj}.$$ (1)

Now, if $N$ is a subset of ${\cal E}$ and $A$ its algebraic span then $M(A)$ is defined by the generators $x_{i j}$ and the relations

$$\mu x_{i j} = x_{i j} \mu \; \; \mbox{ for all } \mu \in N, \; i,j \in \underline{n}.$$ (2)

As consequences one has relations of the same form where $\mu$ runs through all of $A$.