Remember the definition of the complement
of a submodule ![]() in an
in an ![]() -module
-module ![]() and the definition of the evaluation map
and the definition of the evaluation map
Turning to our special situation we first note that
![]() for all
for all
![]() . Since the bilinear form
induced by
. Since the bilinear form
induced by ![]() is nondegenerate, it follows:
is nondegenerate, it follows:
The following fundamental lemma of this section is easy to prove now.
PROOF: According to the definition
![]() if and only if
if and only if
![]() for all
for all
![]() and
and ![]() . Applying (4) this is the case if and only if
. Applying (4) this is the case if and only if
![]() for all
for all ![]() , thus if and only if
, thus if and only if
![]() . The second equation follows from the first by use of
equation (3).
. The second equation follows from the first by use of
equation (3).![]()
Remember that the dual module
![]() of a coalgebra
of a coalgebra ![]() always posseses the structure
of an algebra by use of the convolution product
always posseses the structure
of an algebra by use of the convolution product
Here, we have identified
![]() with its image under the
natural homomorphism
with its image under the
natural homomorphism
![]() . Note that this
construction is functorial. In the special case
. Note that this
construction is functorial. In the special case
![]() we obtain an algebra structure on
we obtain an algebra structure on
![]() . Furthermore
it is easy to show that the evaluation map
. Furthermore
it is easy to show that the evaluation map
![]() is an isomorphism of algebras.
is an isomorphism of algebras.
PROOF: By functoriality the dual map
![]() is an
algebra homomorphism.
Since
is an
algebra homomorphism.
Since
![]() is exact on the right,
is exact on the right, ![]() is injective.
One easily shows
is injective.
One easily shows
![]() . This completes the
proof, since
. This completes the
proof, since
![]() is an algebra isomorphism as mentioned above.
is an algebra isomorphism as mentioned above.![]()
PROOF: This follows immediately from lemmas
3.1 and 3.2.![]()
Now, let us compare the dual of ![]() with
with ![]() . To this aim we
consider the dual map
. To this aim we
consider the dual map
![]() of the inclusion
of the inclusion
![]() .
Because of
.
Because of
![]() for arbitrary
submodules
for arbitrary
submodules ![]() and according to Lemma
3.1 we have
and according to Lemma
3.1 we have
Therefore ![]() factors to an
factors to an ![]() -module homomorphism
-module homomorphism
PROOF: From general results of commutative algebra (cf. [Oe] Anhang A 1.2) it follows
that the torsion submodule of ![]() coincides with
coincides with
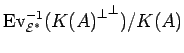 .
By the above calculations this is just the kernel
.
By the above calculations this is just the kernel
![]() of
of ![]() .
.![]()
This immediately implies
At the beginning of this section we have constructed an algebra
structure on the dual module of a coalgebra. Conversely we should obtain
a coalgebra structure on the dual of an algebra ![]() . Whereas this is not
possible in general, it can be done under certain restrictions to
the
. Whereas this is not
possible in general, it can be done under certain restrictions to
the ![]() -module structure of the algebra
-module structure of the algebra ![]() . To be more precise,
the natural
. To be more precise,
the natural ![]() -homomorphism from
-homomorphism from
![]() into
into
![]() must be an isomorphism. This is the case
if
must be an isomorphism. This is the case
if ![]() is projective and finitely generated. Therefore, under these
circumstances the construction is always possible and functorial,
that is: duals of algebra maps become coalgebra maps. Thus we obtain
is projective and finitely generated. Therefore, under these
circumstances the construction is always possible and functorial,
that is: duals of algebra maps become coalgebra maps. Thus we obtain