Change of Base Rings

Let $S$ be another noetherian integral domain together with a homomorphism $R\rightarrow S$ of rings. We will consider $S$ as an $R$-algebra via this homomorphism. In this situation there is a functor from the category of $R$-modules into the category of $S$-modules given by

$${W}^{S}:=S\otimes_{R} W \;\;\mbox{ and } \;\; {\alpha}^{S}:={\rm id}_{S} \otimes \alpha:{U}^{S} \rightarrow {W}^{S}$$ (5)

to each pair of $R$-modules $W$ and $U$ and an $R$-homomorphism $\alpha:U \rightarrow W$. We will study the behaviour of the construction of centralizer coalgebras under these functors. It will turn out that the centralizer coalgebra behaves better than the centralizer algebra. To start with let

$${{\cal E}}_{S} := {\rm End}_{S}{({V}^{S})},\;\; {\zeta}_{S}:{{\cal E}}^{S}\rightarrow {{\cal E}}_{S}$$

where ${\zeta}_{S}$ is given by ${\zeta}_{S}(s \otimes e)(t \otimes v):= st \otimes e(v)$ for all $s,t \in S, e \in {\rm End}_{R}{(V)}, v \in V$. Let $J_{A}:A\hookrightarrow {\cal E}$ be the natural embedding of the subalgebra $A\subseteq {\cal E}$ and let

$${A}_{S}:={\rm im}({\zeta}_{S}\circ{J_{A}}^{S})$$

denote the image of ${A}^{S}$ in ${{\cal E}}_{S}$. Further there are natural homomorphisms

$${\eta}_{S}: {C(A)}^{S} \rightarrow C({A}_{S})={\rm End}_{{A}_{S}}{({V}^{S})}\subseteq {{\cal E}}_{S}$$

on generators given in a similar way to ${\zeta}_{S}$. Note, that both, ${\zeta}_{S}$ and ${\eta}_{S}$ are homomorphisms of algebras connected by the equation

$$J_{C({A}_{S})}\circ {\eta}_{S}={\zeta}_{S} \circ {J_{C(A)}}^{S}.$$

Thus ${\eta}_{S}$ is injective if and only if ${J_{C(A)}}^{S}$ is injective ($J$ stands for the corresponding embeddings). This may fail if $C(A)$ is not a pure $R$-submodule in ${\cal E}$. Further ${\eta}_{S}$ may fail to be surjective (see the example following theorem 4.3). $C(A)$ is called stable under base change if ${\eta}_{S}$ is an isomorphism of for all choices for $S$. Now, in analogy to ${\eta}_{S}$ we are going to consider natural homomorphisms

$${\mu}_{S} : {M(A)}^{S} \rightarrow M({A}_{S})={({{\cal E}}_{S})}^*/K({A}_{S})$$

We will show that they are isomorphisms independent of the choices for $A,\; R$ and $S$. To this claim we consider

$${\chi}_{S}:={{{\zeta}_{S}}^*}^{-1}\circ\psi_{{\cal E}}: {{{\cal E}}^*}^{S}\rightarrow {({{\cal E}}_{S})}^*$$

where $\psi_{{\cal E}}:{{{\cal E}}^*}^{S}\rightarrow {{{\cal E}}^{S}}^*$ is the natural homomorphism given by $\psi_{{\cal E}}(s \otimes f)(t \otimes e):=stf(e)$ on genorators with $s,t \in S, \; f \in {{\cal E}}^* \; e \in W$. It is easy to check that ${\chi}_{S}$ is a homomorphism of coalgebras if the coalgebra structure on ${{{\cal E}}^*}^{S}$ is defined in a canonical way (for details see [Oe] section 1.5). Further, the verification of the commutativity rule

$${\chi}_{S}\circ {{\vartheta}_{tr}}^{S}={{\vartheta}_{tr}}_{S}\circ {\zeta}_{S}$$ (6)

is straightforward, as well. Here ${{\vartheta}_{tr}}_{S}:{{\cal E}}_{S}\rightarrow {({{\cal E}}_{S})}^*$ is the isomorphism induced by the matrix trace map ${tr}_{S}:{{\cal E}}_{S}\rightarrow S$. Setting

$$L({A}_{S}):=<[\nu,\mu ]\vert \nu \in {A}_{S}, \mu \in {{\cal E}}_{S} >_{S -\mbox{mod}},$$

we obtain

$${\rm im}({\zeta}_{S}\circ {J_{L(A)}}^{S})=L({A}_{S}),$$

since ${\zeta}_{S}$ is an isomorphism of $S$-algebras. By definition we have ${K(A)}_{S}={{\vartheta}_{tr}}_{S}({L(A)}_{S})$ and ${\rm im}({J_{K(A)}}^{S})={\rm im}({{\vartheta}_{tr}}^{S}\circ {J_{L(A)}}^{S})$. Using (6) this yields

$${\rm im}({\chi}_{S}\circ {J_{K(A)}}^{S})=K({A}_{S}).$$ (7)

Here again, we have used the symbol $J$ to indicate embeddings of $R$-submodules. Note that in particular $K:= {\rm im}({J_{K(A)}}^{S})$ is a coideal in ${{{\cal E}}^*}^{S}$ since ${\chi}_{S}$ is an isomorphism of coalgebras and therefore ${M(A)}^{S}\cong {{{\cal E}}^*}^{S}/ K$ is a coalgebra. Finally, we are able to define the natural homomorphism ${\mu}_{S}$ as the factorization of ${\chi}_{S}$ which exists by (7). We immediately obtain

Theorem 4.1 (Change of Base Rings)   For any noetherian integral domain $S$ which is an $R$-algebra and any $R$-subalgebra $A$ of ${\cal E}$ there is a natural homomorphism

$${\mu}_{S}:S\otimes_{R}M(A)\rightarrow M(S\otimes_{R} A)$$

which is an isomorphism of $S$-coalgebras.

This means that $M(A)$ is stable under base changes for all choices of $A$ and $R$. If the $R$-algebra $S$ is a field, it follows from theorems 3.3 and 4.1 that

$${\rm dim}_{S}{(C({A}_{S}))}= {\rm dim}_{S}{({M({A}_{S})}^*)}= {\rm dim}_{S}{({({M(A)}^{S})}^*)}={\rm dim}_{S}{({M(A)}^{S})}$$ (8)

Now, for a noetherian integral domain $R$ it is known from commutative algebra that an $R$-module $W$ is projective if and only if the dimension of ${W}^{S}$ is independent of the field $S$. Thus we obtain

Corollary 4.2   Let $F$ be the field of fractions of $R$. Then $M(A)$ is projective if and only if ${\rm dim}_{S}{(C({A}_{S}))}={\rm dim}_{F}{(C({A}_{F}))}$ holds for each field $S$.

Theorem 4.3 (Criterion of Projectivity)   The following statements are equivalent:

(a)

The centralizer coalgebra $M(A)$ is projectiv.

(b)

The centralizer algebra $C(A)={\rm End}_{A}{(V)}$ is stable under base change.

(c)

$M(A)$ is torsion free and $C(A)$ a direct summand in ${\cal E}$.

PROOF: First assume (a). Then the sequence

$$0\rightarrow K(A)\rightarrow {{\cal E}}^*\rightarrow M(A)\rightarrow 0$$

is split and consequently the same is true for

$$0\rightarrow {M(A)}^*\rightarrow {{{\cal E}}^*}^* \rightarrow {{{\cal E}}^*}^*/{K(A)}^{\bot}\rightarrow 0.$$

Since ${\rm Ev}_{{\cal E}}$ induces an isomorphism between ${{{\cal E}}^*}^*/{K(A)}^{\bot}$ and ${\cal E}/C(A)$ according to lemma 3.1 it follows that ${\cal E}/C(A)$ is projective, as well. Thus $C(A)$ is a direct summand in ${\cal E}$ proving (c).

Part (a) follows from (c) by theorem 3.7, since the dual of a projective module is projective again. To verify (b) we therefore may assume both (a) and (c). Since $C(A)$ is a direct summand ${J_{C(A)}}^{S}$ is injective for all $R$-algebras $S$. Consequentely all ${\eta}_{S}$ are injective (see above). To show surjectivity note that the image ${\rm im}({\zeta}_{S} \circ{J_{C(A)}}^{S})= {\rm im}(J_{C({A}_{S})}\circ {\eta}_{S})$ of ${C(A)}^{S}$ in ${{\cal E}}_{S}$ must be a direct summand therein, since ${\zeta}_{S}$ is an isomorphism and ${\rm im}({J_{C(A)}}^{S})$ a direct summand in ${{\cal E}}^{S}$. Therefore, to show that this submodule of ${{\cal E}}_{S}$ coincides with $C({A}_{S})$, it is enough to verify that both have the same rank (the dimension of the $G$-tensored module over the field $G$ of fractions on $S$). But these ranks must indeed be the same as can be seen from the following calculations

$${\rm dim}_{G}{({C(A)}^{G})}={\rm dim}_{F}{({C(A)}^{F})}={\rm dim}_{F}{(C({A}_{F}))}= {\rm dim}_{G}{(C({A}_{G}))}.$$

where the left-hand-side equation holds by projectivity of $C(A)$, the right-hand-side one by corollary 4.2 and the one in the middle since ${\eta}_{F}$ is an isomorphism by flatness of the field $F$ of fractions on $R$. This establishes (b).

Now assume (b). This implies that the map ${J_{C(A)}}^{S}$ induced by the embedding $J_{C(A)}$ is injective for all $S$. By commutative algebra arguments one concludes that $C(A)$ is a direct summand in the $R$-free module ${\cal E}$, in particular it is projective. Now, let $S$ be a field. Since ${\eta}_{S}$ is an isomorphism we have

$${\rm dim}_{S}{({C(A)}^{S})}= {\rm dim}_{S}{(C({A}_{S}))}.$$

The left-hand-side is independent of $S$ by projectivity of $C(A)$. Thus by corollary 4.2 $M(A)$ is projective yielding (a).$\Box$

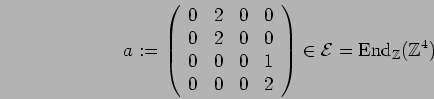
Example: Let $R={\mathbb{Z}}$ and $V={\mathbb{Z}}^4$. Further let

$$a:=\left( \begin{array}{cccc} 0 & 2 & 0 & 0 \\ 0 & 2 & 0 & 0... ... \right)\in {\cal E}={\rm End}_{{\mathbb{Z}}}{({\mathbb{Z}}^4)}$$

and $A:=<a>$ be the subalgebra in ${\cal E}$ generated by $a$. Each field can be considered as a ${\mathbb{Z}}$-algebra. For a field of characteristic different from $2$ the minimum polynomial of ${a}^{S}$ is $t^2-2t$, but in characteristic $2$ it is $t^2$. This means that the algebra ${A}_{S}$ is two dimensional for each field $S$. It follows that $A$ is a direct summand in ${\cal E}$. But nevertheless $M(A)$ is not projective (free), because in the case of a field of characteristic different from $2$ ${a}^{S}$ is diagonalisable and one calculates ${\rm dim}_{S}{(C({A}_{S}))}=2^2+2^2=8$, while in the case of characteristic $2$ we have ${\rm dim}_{S}{(C({A}_{S}))}=9$. Therefore $M(A)$ can't be projective in view of corollary 4.2.