For convenience, in in the following sections we abbreviate ![]() and
denote multiplication in
and
denote multiplication in
![]() by juxtaposition instead of
by juxtaposition instead of ![]() .
Furthermore, to sets
.
Furthermore, to sets
![]() we associate integers
we associate integers
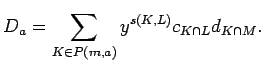
SKETCH OF PROOF: In order to prove this, one has to use a more general statement
in which the set
![]() is substituted by
is substituted by
![]() for some
for some
![]() . After this, the results can be proved
straightforwardly using induction on
. After this, the results can be proved
straightforwardly using induction on ![]() and the relations
(14) and (15) of the exterior algebra.
For the details we refer to
appendix 18.3.
and the relations
(14) and (15) of the exterior algebra.
For the details we refer to
appendix 18.3.
![]()
To a set
![]() we associate the followng subsets of
we associate the followng subsets of
![]() :
:
PROOF: We apply Lemma 13.1 to
![]() and
and
![]() . Since
. Since
![]() there is an invertible element
there is an invertible element
![]() such that
such that
![]() by (13). We claim
that
by (13). We claim
that
![]() vanishes for each
vanishes for each
![]() that
is not contained in
that
is not contained in
![]() .
If
.
If
![]() then
then
![]() .
If
.
If
![]() and
and
![]() then
then
![]() .
Finally if
.
Finally if
![]() and
and
![]() then
then
![]() .
Thus the expression is nonzero only if
.
Thus the expression is nonzero only if
![]() .
A set
.
A set
![]() is obviously contained in
is obviously contained in ![]() , so
by the second part of the Lemma we have
, so
by the second part of the Lemma we have
![]() . Thus, setting
. Thus, setting ![]() the assertion
follows.
the assertion
follows.
![]()
PROOF: Clearly the sum is ![]() if
if ![]() since
since
![]() . For
. For ![]() we show by induction on
we show by induction on ![]() that the sum is zero.
Starting with the case
that the sum is zero.
Starting with the case ![]() we have
we have
![]() and
and
![]() . For the induction step,
let
. For the induction step,
let
![]() be minimal and set
be minimal and set
![]() .
If
.
If
![]() we calculate
we calculate
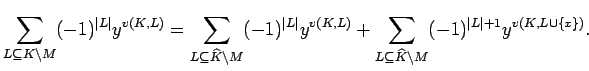
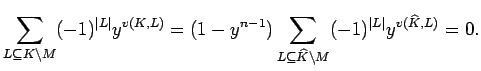
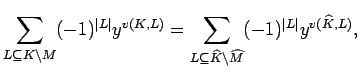
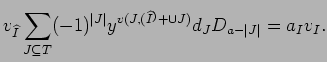
PROOF: Let
![]() and
observe that
and
observe that
![]() ,
,
![]() ,
,
![]() and that
and that
![]() .
Because
.
Because ![]() , we must have
, we must have ![]() . On the other hand
. On the other hand
![]() implies
implies
![]() for a set
for a set
![]() as in the sum. Therefore we may apply Lemma
13.2:
as in the sum. Therefore we may apply Lemma
13.2:
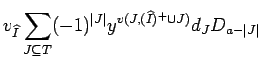 |
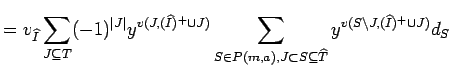 |
|
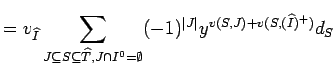 |
||
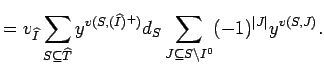 |
But by Lemma 13.3, the last term equals
![]() . Using relation (13)
of the exterior algebra, this can be transformed into
. Using relation (13)
of the exterior algebra, this can be transformed into
![]() up to some invertible mutiple
up to some invertible mutiple ![]() .
.
![]()
We are now able to prove Proposition 12.1 by induction
on the Lie rank ![]() . In the case where
. In the case where ![]() both sets of
both sets of
![]() are reverse symplectic. In
are reverse symplectic. In
![]() there is just one set
namely
there is just one set
namely ![]() , for which we have
, for which we have
![]() . Thus there is nothing to prove here.
. Thus there is nothing to prove here.
For the induction step we embed
![]() into
into
![]() sending
sending ![]() to
to
![]() . It is easy to check that this indeed leads to an embedding of
algebras. Using the induction hypothesis we may treat the
case where
. It is easy to check that this indeed leads to an embedding of
algebras. Using the induction hypothesis we may treat the
case where
![]() without much effort.
Some caution is needed only concerning the difference
between the two ideals
without much effort.
Some caution is needed only concerning the difference
between the two ideals ![]() of
of
![]() and
and
![]() . Denote them by
. Denote them by ![]() and
and ![]() . A single element
. A single element
![]() can be
written
can be
written
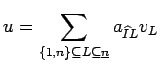 mod
mod
where the basis elements ![]() all are smaller than
all are smaller than ![]() , that is
, that is
![]() for the corresponding multi-indices.
If
for the corresponding multi-indices.
If
![]() we may apply the induction hypothesis
to the
set
we may apply the induction hypothesis
to the
set
![]() in case
in case
![]() is non reverse symplectic too:
is non reverse symplectic too:
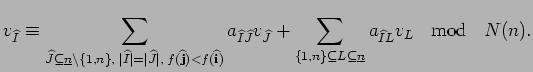
Again, the second sum compensate for
the difference between the
two ideals ![]() and
and ![]() .
Multiplying this congruence by
.
Multiplying this congruence by ![]() from the left (respectively by
from the left (respectively by ![]() from the right,
respectively by both from both sides) yields the assertion because
the elements
from the right,
respectively by both from both sides) yields the assertion because
the elements ![]() vanish, and
vanish, and
![]() implies
implies
![]() ,
where
,
where ![]() is the multi-index attached to the set
is the multi-index attached to the set
![]() .
.
It remains to prove the assertion in the
case where
![]() is reverse symplectic.
Here we need the preparations of this section.
By the reverse symplectic condition applied to tableaux of shape
is reverse symplectic.
Here we need the preparations of this section.
By the reverse symplectic condition applied to tableaux of shape ![]() we have
we have
![]() for all
for all ![]() , where
, where
![]() .
Because
.
Because ![]() itself is non reverse symplectic we must have
itself is non reverse symplectic we must have
![]() . According to Lemma 13.4
we conclude
. According to Lemma 13.4
we conclude
![]() . But this implies the assertion of Proposition
12.1 in the remaining case too.
. But this implies the assertion of Proposition
12.1 in the remaining case too.