First, we have to state the ![]() -analogue of [O2, Lemma 8.1],
one of the principal ingredients in the
proof of the symplectic straightening algorithm in the classical
case.
In order to define the quantum analogue to the ideal
-analogue of [O2, Lemma 8.1],
one of the principal ingredients in the
proof of the symplectic straightening algorithm in the classical
case.
In order to define the quantum analogue to the ideal ![]() considered
there
we have to look in more detail at the elements
considered
there
we have to look in more detail at the elements ![]() and
and ![]() defined
in the previous section.
defined
in the previous section.
Relation (16) implies
![]() . Consequently
we get from (14) and (15)
. Consequently
we get from (14) and (15)
This stands in remarkable contrast to the classical and even
quantum linear case where such expressions vanish. On the other hand by
(13) and the above explanations
the elements ![]() and
and ![]() commute with each other, exactly as in the
classical case. Consequently, the elements
commute with each other, exactly as in the
classical case. Consequently, the elements
![]()
![]() are defined
independently of the order of the elements of the subset
are defined
independently of the order of the elements of the subset
![]() .
Again, we write
.
Again, we write
![]() for the collection of all subsets
for the collection of all subsets ![]() of
of
![]() whose cardinality is
whose cardinality is ![]() . Set
. Set
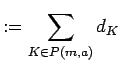
and let
![]() be the ideal in
be the ideal in
![]() generated by the elements
generated by the elements
![]() .
We call an ordered subset
.
We call an ordered subset
![]() reverse symplectic if the multi-index
reverse symplectic if the multi-index ![]() obtained from
obtained from ![]() by ordering its elements according to
by ordering its elements according to ![]() (obtained from
(obtained from
![]() by a suitable permutation
by a suitable permutation
![]() such that
such that
![]() ) is
) is
![]() -reverse symplectic standard. Here
-reverse symplectic standard. Here ![]() is the
is the ![]() -th
fundamental weight.
-th
fundamental weight.
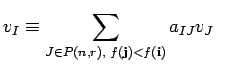 mod
mod
We postpone the very technical proofs of
both propositions to separate sections below.
Let us prove Proposition 8.3 in
the case
![]() , first. Take
, first. Take
![]() . Using the weak part of the
straightening algorithm 10.1, we may
assume
. Using the weak part of the
straightening algorithm 10.1, we may
assume
![]() .
This means
.
This means
![]() . In order to apply
our lemmas
we have to change orders from
. In order to apply
our lemmas
we have to change orders from ![]() to
to ![]() . Let
. Let
![]() be such that
be such that
![]() , that is,
, that is, ![]() is a multi-index corresponding to a non reverse
symplectic ordered set
is a multi-index corresponding to a non reverse
symplectic ordered set
![]() in the sense of Proposition
in the sense of Proposition ![]() . Application of this proposition to
. Application of this proposition to ![]() yields
yields
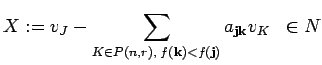
since
![]() .
According to Proposition 12.2, the element
.
According to Proposition 12.2, the element
![]() must be zero. Applying (11.6),
we obtain the following equation holding in
must be zero. Applying (11.6),
we obtain the following equation holding in
![]() :
:
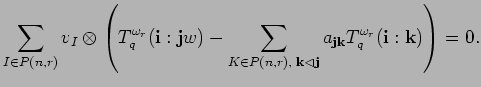
Since
![]() is a basis of
is a basis of
![]() , each
individual summand in the summation over
, each
individual summand in the summation over
![]() must be zero.
Together with Corollary 9.12,
this gives the desired result in the case of multi-indices
must be zero.
Together with Corollary 9.12,
this gives the desired result in the case of multi-indices ![]() corresponding to ordered subsets
corresponding to ordered subsets
![]() , that is
, that is
![]() . The case for general
. The case for general ![]() can be
deduced from this using
can be
deduced from this using
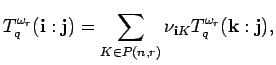
which follows from the formula
![]() of Lemma 11.7
together with (19).
of Lemma 11.7
together with (19).
Next we consider the general case of ![]() . Here, we can proceed
exactly as in the classical case.
Again, we may assume
. Here, we can proceed
exactly as in the classical case.
Again, we may assume
![]() by the weak part of the
straightening algorithm. Let
by the weak part of the
straightening algorithm. Let
![]() be the dual partition (
be the dual partition (
![]() ). We split
). We split ![]() into
into ![]() multi-indices
multi-indices
![]() , where for
each
, where for
each
![]() the entries of
the entries of ![]() are taken from the
are taken from the ![]() -th
column of
-th
column of
![]() . The same thing can be done with
. The same thing can be done with
![]() . Since
. Since ![]() is not
is not ![]() -reverse
symplectic standard but standard
there must be a column
-reverse
symplectic standard but standard
there must be a column ![]() such that
such that ![]() is not
is not
![]() -reverse symplectic standard. Applying the result to the
known case of
-reverse symplectic standard. Applying the result to the
known case of
![]() , we obtain
, we obtain
The element
![]() satisfies
satisfies
![]() ,
,
![]() is constructed from
is constructed from ![]() by replacing the
entries of
by replacing the
entries of ![]() by that of
by that of ![]() and
and
![]() is
the same as
is
the same as
![]() for the corresponding
for the corresponding ![]() .
The product formula for bideterminants applied above is valid by our choice
of basic
.
The product formula for bideterminants applied above is valid by our choice
of basic ![]() -tableaux inserting the numbers
-tableaux inserting the numbers
![]() column by column top down (otherwise the non-commutativity of
column by column top down (otherwise the non-commutativity of
![]() would cause some trouble). From (11) we see
would cause some trouble). From (11) we see
![]() and the proof of 8.3
is completed.
and the proof of 8.3
is completed.