In order to prove the proposition
we have to consider generalizations of the
elements
![]() , which are defined for any
, which are defined for any ![]() by
by
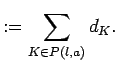
For a positive integer ![]() , define the
, define the ![]() -integer
-integer
![]()
![]() .
.
PROOF: Using the above introduced notations we may write the right hand side
of (22) as
![]() . Since
. Since
![]() , we deduce
, we deduce
![]() modulo
modulo ![]() if
if ![]() and
and
![]() modulo
modulo ![]() in the case
in the case ![]() .
.
We proceed by induction on ![]() . If
. If ![]() , both sides are zero if
, both sides are zero if ![]() .
In the case
.
In the case ![]() we have to show that
we have to show that
![]() which was proved above.
which was proved above.
For the induction step we write
![]() and obtain
and obtain
Since
![]() the lemma follows.
the lemma follows.
![]()
We introduce some new conventions. To an ordered
subset
![]() we define corresponding multi-indices by
we define corresponding multi-indices by
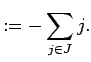
From the definition of ![]() , we have
, we have
![]() .
By the relations of the exterior algebra there is another integer
.
By the relations of the exterior algebra there is another integer
![]() such that
such that
![]() .
By (11.6) and Corollary 11.9 we calculate
.
By (11.6) and Corollary 11.9 we calculate
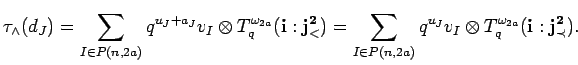
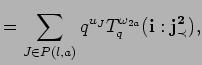
We will prove the equation
![]() with the help of the Laplace-Expansion which
is a special case of Laplace-Duality (Proposition
9.7) applied to the partitions
with the help of the Laplace-Expansion which
is a special case of Laplace-Duality (Proposition
9.7) applied to the partitions
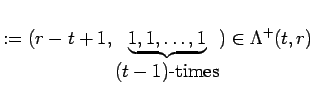
Caution: The symbol should not be confused with the ![]() -th component
of a partition
-th component
of a partition ![]() .
A bideterminant
.
A bideterminant
![]() is the product of
a
is the product of
a
![]() minor determinant with a monomial, that is
minor determinant with a monomial, that is
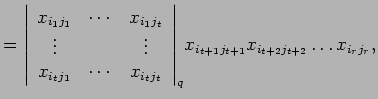 |
in particular
![]() .
.
Let ![]() denote the set of distinguished left coset representatives
of
denote the set of distinguished left coset representatives
of
![]() in
in
![]() . Using basic transpositions
. Using basic transpositions
![]() this set can be written down explicitly:
this set can be written down explicitly:
Setting
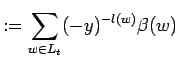
the quantum symplectic (left) Laplace-Expansion deduced from Proposition 9.7 reads
In the classical case and ![]() this turns out to be the familar Laplace-Expansion.
There is a very useful recursive calculation rule for the endomorphisms
this turns out to be the familar Laplace-Expansion.
There is a very useful recursive calculation rule for the endomorphisms
![]() :
:
Before we state the fundamental lemma of this section we remind the
reader of the addition of multi-indices, for example
![]() .
.
PROOF: First we treat the case where ![]() .
Here we have
.
Here we have
![]() by definition. Since
by definition. Since
![]() the summation on the
right hand side of the lemma is over
the summation on the
right hand side of the lemma is over
![]() too. Furthermore,
too. Furthermore,
For the general case we use induction on ![]() . In the case
. In the case ![]() we
necessarily have
we
necessarily have ![]() , which has been treated above.
In order to prove the induction
step we may assume
, which has been treated above.
In order to prove the induction
step we may assume ![]() and
and ![]() . We
divide the summation on the right hand side
into three subsums:
. We
divide the summation on the right hand side
into three subsums:
(A) ![]() (B)
(B)
![]() (C)
(C)
![]()
and write ![]() ,
, ![]() and
and ![]() respectively.
First we treat subsum
respectively.
First we treat subsum ![]() .
Using (4.2) we see
.
Using (4.2) we see
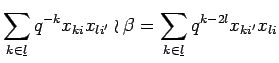
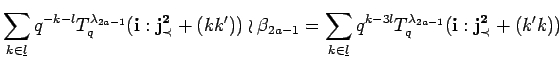
If
![]() contains
contains ![]() , we may write
, we may write
![]() with some
with some
![]() such that for the corresponding
multi-index
such that for the corresponding
multi-index
![]() we have
we have
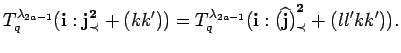
The bideterminant
![]() vanishes by Corollary 9.2. Unfortunately the
bideterminant with
vanishes by Corollary 9.2. Unfortunately the
bideterminant with ![]() is not zero in general.
Since
is not zero in general.
Since
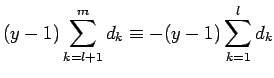 mod
mod 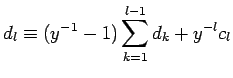 mod
mod
Since
![]() and
and
![]() by (17)
we may again deduce from Corollary 11.9
that
by (17)
we may again deduce from Corollary 11.9
that
Here, in addition, we have used the equations
![]() and
and
![]() which are valid inside the exterior algebra.
Modulo the ideal
which are valid inside the exterior algebra.
Modulo the ideal
![]() of
of
![]() spanned by
spanned by ![]() the congruence relation
the congruence relation
![]() holds. Therefore, modulo this ideal
the congruence
holds. Therefore, modulo this ideal
the congruence
by Lemma 9.3. Here we have also used the fact that
![]() by Lemma 9.4 since
by Lemma 9.4 since
![]() .
Now substitute (27) into the first equation of
(26) and the equations (26)
and (25) into (24). Note that the terms
comming from
(25) and the last term of (27) cancel each
other. We obtain the following expression for the subsum (A).
.
Now substitute (27) into the first equation of
(26) and the equations (26)
and (25) into (24). Note that the terms
comming from
(25) and the last term of (27) cancel each
other. We obtain the following expression for the subsum (A).
Now we apply Laplace-Expansion (Proposition 14.3) twice to the first and second bideterminant and once to the third:
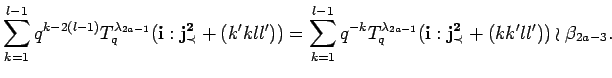
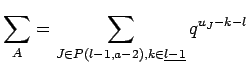 |
||
To the first term of that sum we can apply the induction hypothesis. To this claim
note that the symbol ![]() on the left of the bideterminant stands for a sum
over the bideterminant's left multi-index. In order to apply the induction hypothesis
this summation has to be commuted with the summation under the
on the left of the bideterminant stands for a sum
over the bideterminant's left multi-index. In order to apply the induction hypothesis
this summation has to be commuted with the summation under the ![]() -symbol.
In a similar way we can apply Lemma 14.1
together with Corollary 11.9 to the second term of the
sum above. This results in
-symbol.
In a similar way we can apply Lemma 14.1
together with Corollary 11.9 to the second term of the
sum above. This results in
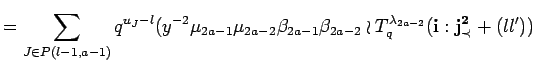 |
||
Since
![]() and
and
![]() commute, we see from equation (23)
commute, we see from equation (23)
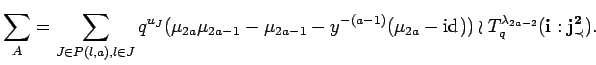
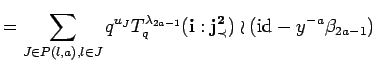 |
||
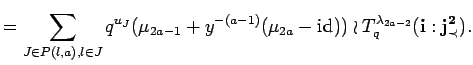 |
Thus subsum (A) and (B) together equal
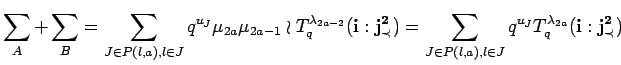

Now we are able to prove Proposition 12.2. As we
have seen above, we have to show
![]() for
for
![]() and
and
![]() . From (4.3)
we already know
. From (4.3)
we already know
![]() for all
for all
![]() .
We will deduce the general case by induction on a with the help of
Lemma 14.4. Let
.
We will deduce the general case by induction on a with the help of
Lemma 14.4. Let ![]() and
and
![]() be arbitrary. We apply Laplace-Expansion to the
formula of the lemma:
be arbitrary. We apply Laplace-Expansion to the
formula of the lemma:
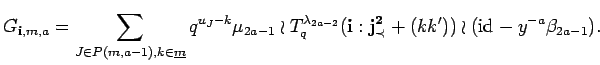
As in the proof of the lemma we may commute
![]() to the other side of the bideterminant. Let
to the other side of the bideterminant. Let
![]() be the
coefficient matrix of the endomorphism
be the
coefficient matrix of the endomorphism
![]() with respect to the canonical basis. We denote the multi-index consisting
of the first
with respect to the canonical basis. We denote the multi-index consisting
of the first ![]() indices of
indices of ![]() by
by
![]() and obtain
and obtain
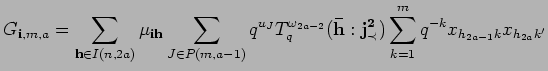
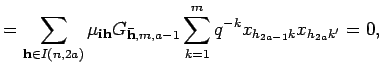
since
![]() for all
for all
![]() by the
induction hypothesis.
by the
induction hypothesis.