In [GL] Graham and Lehrer have presented
a nice criterion for quasi-heridity of a cellular algebra
which we will now verify in our case.
This will prove Theorem
7.5.
To this aim we have to investigate the
bilinear form
![]() on the
standard modules
on the
standard modules
![]() . We must show that they are not zero
([GL, 3.10]). Let us first calculate
the Grammatrix of
. We must show that they are not zero
([GL, 3.10]). Let us first calculate
the Grammatrix of
![]() with respect to
the basis
with respect to
the basis
![]() of
of
![]() . We abbreviate its entries by
. We abbreviate its entries by
![]() . According to the
definition in [GL, 2.3], these numbers satisfy
. According to the
definition in [GL, 2.3], these numbers satisfy
Such a congruence relation is valid with
![]() being
independent of
being
independent of ![]() and
and ![]() by the axioms of a cellular algebra
(see [GL, 1.7]). Dualizing this congruence we obtain the following
counterpart in the cellular coalgebra
by the axioms of a cellular algebra
(see [GL, 1.7]). Dualizing this congruence we obtain the following
counterpart in the cellular coalgebra
![]() :
:
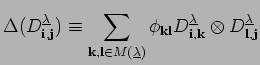
modulo
![]() . According to the calculations
for the verification of axiom
. According to the calculations
for the verification of axiom ![]() in the previous section
we see using the notations from there that
in the previous section
we see using the notations from there that
The bilinear form
![]() is different from zero if this is the case
for a single entry
is different from zero if this is the case
for a single entry
![]() . We calculate
. We calculate
![]() where
where
![]() is the
is the ![]() -tableau
-tableau
![]() with constant rows
with constant rows
![]() for all
for all
![]() and
and
![]() .
Obviously
.
Obviously ![]() is a standard tableau with respect to both orders on n, namely
is a standard tableau with respect to both orders on n, namely
![]() as well as
as well as ![]() . Furthermore the reverse symplectic condition holds
because
. Furthermore the reverse symplectic condition holds
because
![]() . Consequently we have
. Consequently we have
![]() . Note that
. Note that
![]() does not contain any pair of associated indices
does not contain any pair of associated indices
![]() . The content
. The content
![]() of
of ![]() is given by
is given by
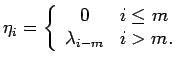
Consider the endomorphism
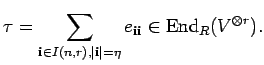
It is easy to see that ![]() commutes with
commutes with ![]() and
and ![]() for all
for all
![]() . Consequently it is an endomorphism of the
. Consequently it is an endomorphism of the
![]() comodul
comodul
![]() (in fact it is the idempotent of
(in fact it is the idempotent of
![]() corresponding to the weightspace with weight
corresponding to the weightspace with weight ![]() ). There is an induced
action of
). There is an induced
action of ![]() on
on
![]() from the right defined by
from the right defined by
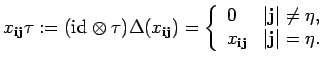
For a bideterminant we have
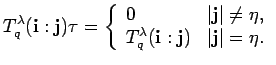
Applying ![]() to the defining equation (30) of
to the defining equation (30) of
![]() we see that
we see that
![]() if
if
![]() by linear independence of
by linear independence of
![]() .
Since
.
Since ![]() is the only element in
is the only element in
![]() having
content
having
content ![]() it follows
it follows
![]() if
if
![]() and
we conclude
and
we conclude
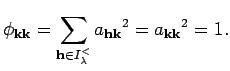
By [GL, Remark 3.10], this finishes the proof of Theorem 7.5.