Results

Let us first describe what we will take for the set $\Lambda$ occuring in the definition of the cellular coalgebra:

$$\Lambda :=\{ {\underline{\lambda}}$$$$\mbox{\index{${\underline{\lambda}}$}}$$$$:=(\lambda,l)\vert\; 0\leq l \leq \frac r2, \; \lambda \in \Lambda^+(m, r-2l) \}.$$

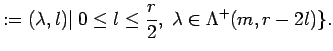
According to the definition of a cellular coalgebra to each $\underline{\lambda}=(\lambda, l) \in \Lambda$ a set $M(\underline{\lambda})$ must be assigned. We take:

$$M(\underline{\lambda}):= I_{\lambda}^{\rm mys}.$$

Finally the basis elements themselves are defined by

$$D^{\underline{\lambda}}_{{\bf i}, {\bf j}}:={d_q}^lT^{\lambda}_q({\bf i}:{\bf j}).$$

Now, our principal aim is to prove the following

Theorem 7.1   The $R$-module $A^{{\rm s}}_{R,q}(n,r)$ has a basis given by

$${{\bf B}_r}$$$$\mbox{\index{${{\bf B}_r}$}}$$$$:= \{ D^{\underline{\lambda}}_{{\bf i}, {\bf j}}\vert\; \underline{\lambda}\in \Lambda, {\bf i}, {\bf j} \in M(\underline{\lambda}) \}.$$

Furthermore, the unique $R$-linear map $^*$ with ${D^{\underline{\lambda}}_{{\bf i}, {\bf j}}}^*= D^{\underline{\lambda}}_{{\bf j}, {\bf i}}$ is an involutory coalgebra anti-automorphism and the axioms of a cellular coalgebra are satisfied.

By Proposition 5.1 we may conclude immediately:

Theorem 7.2   The symplectic $q$-Schur algebra $S^{\rm s}_{R,q}(n,r)$ is a cellular algebra with the basis dual to ${\bf B}_r$ as a cellular basis.

Another direct consequence of 7.1 can be obtained from [O2, Theorems 3.3 and 4.3].

Theorem 7.3   The symplectic $q$-Schur algebra is stable under base change and it is identical with the centralizer of the algebraic span ${\cal A}_r$ of the endomorphism $\beta_i$ and $\gamma_i$.

Remark 7.4   The theorem sets $S^{\rm s}_{R,q}(n,r)$ into relation with the Birman-Murakami-Wenzl algebra since $\beta_i$ and $\gamma_i$ define a representation of it on $V^{\otimes r}$ (cf. [O1, Satz 2.2.3]).

At the end of this paper we will improve 7.2 by showing that the bilinear form $\phi_{\lambda}$ on the standard modules $W_{\lambda}$ is nonzero for each $\lambda$. By [GL, 3.10] this means

Theorem 7.5   The symplectic $q$-Schur algebra $S^{\rm s}_{R,q}(n,r)$ is integrally quasi-hereditary.

Let us first see how the involution of Theorem 7.1 arises. It realizes matrix transposition for our quantum monoid. On the generators $x_{{\bf i} {\bf j}}$ this transposition map is defined as in the classical case by ${x_{{\bf i} {\bf j}}}^*:=x_{{\bf j} {\bf i}}$. Indeed, this gives a well defined algebra map on $A^{{\rm s}}_{R,q}(n)$, since the coefficient matrices of $\beta$ and $\gamma$ are symmetric (i.e. $\beta_{{\bf i}{\bf j}}= \beta_{{\bf j}{\bf i}}$ and $\gamma_{{\bf i}{\bf j}}=\gamma_{{\bf j}{\bf i}}$) implying $({\beta \wr x_{{\bf i} {\bf j}}})^*=x_{{\bf j} {\bf i}}\wr \beta$ and $({\gamma \wr x_{{\bf i} {\bf j}}})^*=x_{{\bf j} {\bf i}}\wr \gamma$ and thus, keeping the relations of that algebra fixed. Furthermore, the endomorphisms $\kappa_{\lambda}\in {\rm End}_{R}{(V^{\otimes r})}$ must have symmetric coefficient matrices, as well. We calculate

$${t_q^{\lambda}({\bf i}:{\bf j})}^*= ({\kappa_{\lambda}\wr x_{{\... ...})^*= x_{{\bf j} {\bf i}}\wr \kappa_{\lambda}= t_q^{\lambda}({\bf j}:{\bf i})$$ (8)

and in a similar way ${d_q}^*=d_q$ holds by definition (7). This shows, that $^*$ factors to an algebra map of $A^{{\rm s}}_{R,q}(n)$. From the comultiplication rule (4) it directly follows that $^*$ is an anti-coalgebra map. This implies axiom (C2*) of a cellular coalgebra.

The verification of axiom (C3*) is the second easiest step in the proof of Theorem 7.1, but we will give it at the end of the paper since some additional ingredients are needed. The first statement of this theorem, which is axiom (C1*), is the really hard one. It is the $q$-analogue of [O2, Theorem 6.1]. To prove it we will proceed in a similar way as there. The difficulty is to show that ${\bf B}_r$ is a set of generators. For that purpose the most important step is a quantum symplectic version of the famous straightening formula.