Finishing the proof of Theorem 7.1

Let us briefly recall what we have done so far. With respect to the proof that ${\bf B}_r$ is a basis, we have reduced the fact that it is a set of generators in section 8 to the verification of Proposition 8.1, which we just have completed. Further we already know from section 6 that the axiom $(C2^*)$ of a cellular coalgebra is valid. It remains to show axiom $(C3^*)$ and the fact that ${\bf B}_r$ is linearly independent.

Let us start with the latter task. It is clearly enough to consider the case where $R={\cal Z}={\mathbb{Z}}\,[q,q^{-1}]$. Let ${\mathbb{K}}\,$ be the field of fractions on ${\cal Z}$ and let $\epsilon$ be the image of $q$ under the embedding of ${\cal Z}$ into ${\mathbb{K}}\,$. Any relation among elements of ${\bf B}_r$ with coefficients from ${\cal Z}$ is a relation with coefficients from the field ${\mathbb{K}}\,$ too. Thus, we only have to show $\vert{\bf B}_r\vert=\dim_{{\mathbb{K}}\,} A^{{\rm s}}_{{\mathbb{K}}\,, \epsilon}(n,r)$. Now, $A^{{\rm s}}_{{\mathbb{K}}\,,\epsilon}(n,r)$ is the centralizer coalgebra of the algebra ${\cal A}_{r}$ generated by the endomorphisms $\beta_i$ and $\gamma_i$ acting on $V^{\otimes r}$ in the sense of [O2, Section 2]. Consequently, by the comparison theorem [O2, Theorem 3.3] the dimension in question is the same as the dimension of the centralizer algebra of ${\cal A}_{r}$ acting on $V^{\otimes r}$.

The latter dimension can be deduced from well-known results from the theory of quantum groups. We will use [CP, Theorem 10.2.5 ii, second statement]. The operator called $I_{\epsilon}^{ii+1}$ there equals our $\epsilon^{-1}\beta_i$ thus $\epsilon I_{\epsilon}^{ii+1}=\beta_i$. The application of the theorem shows that the centralizer of our algebra ${\cal A}_{r}$ is identical to the image of the quantized universal enveloping algebra (QUE) corresponding to the Dynkin diagram $C_m$ under its action on $V^{\otimes r}$. Now, by [CP, Proposition 10.1.13 and Theorem 10.1.14], the tensor space $V^{\otimes r}$ decomposes into irreducibles as a QUE-module because $\epsilon \in {\mathbb{K}}\,$ is transcendental over ${\mathbb{Q}}\,$. These irreducibles are indexed by the highest weights of the symplectic group and their dimensions are the same as in the classical case. The weights occurring are the same as for the symplectic group as well and correspond precisely to the elements of the set $\Lambda$ from the definition of ${\bf B}_r$ (cf. [O2, 7.1]). It follows from work of R.C. King that the dimensions of the irreducibles are just $\vert M(\lambda)\vert$ ([Ki],cf. [Do2]). Consequently, we obtain the required identity:

$$\dim_{{\mathbb{K}}\,}{A^{{\rm s}}_{{\mathbb{K}}\,, \epsilon}(n,r)} =\sum_{\lambda \in \Lambda} \vert M(\lambda )\vert^2 = \vert{\bf B}_r \vert.$$

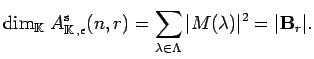
We now verify axiom $(C3^*)$. We abbreviate ${\cal K}:=A^{{\rm s}}_{R,q}(n,r)$. Let $D^{\underline{\lambda}}_{{\bf i}, {\bf j}}\in {\bf B}_r$ where ${\underline{\lambda}}$$:=(\lambda, l)\in \Lambda$ and ${\bf i}, {\bf j}\in M(\lambda)$. As $d_q^l$ is grouplike and $\Delta$ a homomorphism of algebras we calculate using (20) that

$$\Delta (D^{\underline{\lambda}}_{{\bf i}, {\bf j}})=(d_q^l\otimes... ...mbda}}_{{\bf i}, {\bf h}}\otimes D^{\underline{\lambda}}_{{\bf h}, {\bf j}}.$$

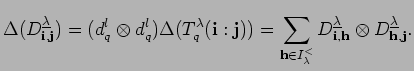
Here, as in section 11, $I_{\lambda}^{<}$ is the set of multi-indices that are $\lambda$-column-standard with respect to the usual order $<$ on $\underline{n}$ (see section 8). Now, according to the straightening formula 8.1 (after application of $^*$) to each ${\bf h}\in I_{\lambda}^{<}$ and ${\bf k}\in M(\lambda)$ there is an element $a_{{\bf h}{\bf k}}\in R$ (unique by the linear independence of ${\bf B}_r$) such that

$$D^{\underline{\lambda}}_{{\bf h}, {\bf j}}\equiv\sum_{{\bf k}\in M(\lambda)} a_{{\bf h}{\bf k}}D^{\underline{\lambda}}_{{\bf k}, {\bf j}}\;\; \;\; {\cal K}(>\underline{\lambda}).$$ (29)

We set

$$h({\bf k},{\bf i}):=\sum_{{\bf h}\in I_{\lambda}^{<} } D^{\unde... ...\bf i}, {\bf h}} a_{{\bf h}{\bf k}}\;\; \in {\cal K}(\geq\underline{\lambda})$$

and obtain

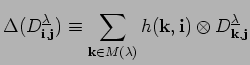$$\Delta (D^{\underline{\lambda}}_{{\bf i},{\bf j}})\equiv\sum_{{\b... ...lambda)} h({\bf k}, {\bf i})\otimes D^{\underline{\lambda}}_{{\bf k}, {\bf j}}$$    mod $$\;\; {\cal K}(\geq\underline{\lambda})\otimes {\cal K}(>\underline{\lambda}).$$

This completes the verification of axiom $(C3^*)$ and hence the proof of Theorem 7.1.