In the classical case symplectic versions of the straightening formula
have already been given in [Co, 2.4] and
[O2, section 7]. In principle, we will
follow the lines of the latter paper.
But there are a lot of additional difficulties,
one of which forces us to work with a reversed version of ![]() -symplectic
standard tableaux.
To prepare for the statement, we define the algebra
-symplectic
standard tableaux.
To prepare for the statement, we define the algebra
by factoring out the ideal generated by the quantum coefficient of dilation.
Since ![]() is homogeneous this algebra is again graded. Let us abbreviate
its
is homogeneous this algebra is again graded. Let us abbreviate
its ![]() -th homogeneous summand by
-th homogeneous summand by
![]()
![]() .
Since
.
Since ![]() is grouplike the comultiplication
is grouplike the comultiplication ![]() obviously factors to
obviously factors to
![]() and
and
![]() . But
. But
![]() is not a bialgebra and
is not a bialgebra and
![]() are not coalgebras, because the augmentation map
are not coalgebras, because the augmentation map ![]() does not factor. In the classical case if
does not factor. In the classical case if ![]() is a field
is a field
![]() equals the coordinate
ring of the symplectic semigroup
equals the coordinate
ring of the symplectic semigroup
![]()
![]() by [O2, remark 7.5]. The missing augmentation map corresponds
to the missing unit element in the semigroup. Therefore we call
by [O2, remark 7.5]. The missing augmentation map corresponds
to the missing unit element in the semigroup. Therefore we call
![]() a semi bialgebra.
a semi bialgebra.
We put an order on the set
![]() of all
partitions of
of all
partitions of ![]() , writing
, writing
![]() if and only if
if and only if ![]() occurs before
occurs before ![]() in the lexicographic order.
In this order the fundamental weight
in the lexicographic order.
In this order the fundamental weight
![]()
![]() is the largest element, whereas
is the largest element, whereas
![]()
![]() is the
smallest one. We define
is the
smallest one. We define
![]() (resp.
(resp.
![]() ) to be the
) to be the ![]() -linear span in
-linear span in ![]() of all
bideterminants
of all
bideterminants
![]() such that
such that
![]() (resp.
(resp.
![]() )(cf. axiom (C3*) of a cellular coalgebra).
Clearly
)(cf. axiom (C3*) of a cellular coalgebra).
Clearly
![]() .
.
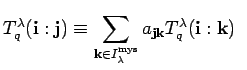 mod
mod Before starting to prove this, we deduce its most important consequence:
PROOF: From the fact that ![]() is central in
is central in
![]() by Remark 4.1 we see that
multiplication by
by Remark 4.1 we see that
multiplication by ![]() from the right (written as
from the right (written as ![]() below)
leads to an exact sequence
below)
leads to an exact sequence
for ![]() .
Therefore, using induction on
.
Therefore, using induction on ![]() we can reduce to showing that
we can reduce to showing that
is a set of generators for
![]() . For this claim it is
enough to show that
. For this claim it is
enough to show that
is a set of generators of
![]() for each partition
for each partition
![]() . To get the last claim from the
straightening formula 8.1, observe that
the involution
. To get the last claim from the
straightening formula 8.1, observe that
the involution ![]() is well defined on
is well defined on
![]() since
since
![]() (see section 7).
Applying
(see section 7).
Applying ![]() to the congruence relation of Proposition 8.1,
one obtains another such formula in which the roles of
to the congruence relation of Proposition 8.1,
one obtains another such formula in which the roles of ![]() and
and
![]() are exchanged. This shows that
are exchanged. This shows that
![]() is indeed a set of
generators for
is indeed a set of
generators for
![]() .
.
![]()
In order to prove the quantum symplectic straightening
formula we need a corresponding
algorithm. Its classical counterpart is [O2, Proposition 7.3].
We define a map
![]() by
by
![]() , where
, where
and order
![]() writing
writing
![]() if and only if
if and only if
![]() appears before
appears before
![]() in the lexicographic order (induced by the ordinary
order on
in the lexicographic order (induced by the ordinary
order on
![]() ). Next, we
obtain an order
). Next, we
obtain an order ![]() on
on
![]() defined by:
defined by:
Here, we have denoted by ![]() the lexicographic order on
the lexicographic order on ![]() induced by our special
order
induced by our special
order ![]() on
on
![]() .
Finally, we obtain a second order
.
Finally, we obtain a second order ![]() on
on ![]() via the embedding
via the embedding
![]() given by
given by
![]() . Now we are able to state the symplectic
straightening algorithm.
. Now we are able to state the symplectic
straightening algorithm.
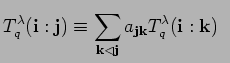 mod
mod
Clearly, the straightening formula 8.1 is
an easy consequence of the above proposition since the set ![]() is finite and therefore the elimination of multi-indices
is finite and therefore the elimination of multi-indices ![]() , that are not
, that are not
![]() -reverse symplectic standard in an expression
-reverse symplectic standard in an expression
![]() must terminate.
must terminate.
The proof of the straightening algorithm will take several sections.
In principle we will proceed in a similar way as in [O2] to prove this
algorithm,
but complications arise because the embedding of
the symplectic group into the general linear group does not extend to quantum
groups. Instead of [O2, Proposition 7.2] we have to establish a
weak form of the quantum symplectic straightening algorithm in a first step.
More precisely, we will first prove 8.3,
where
![]() is substituted by
is substituted by
![]() .
We start with some technical tools.
.
We start with some technical tools.