The calculus of bideterminants is needed inside
![]() .
Unless otherwise stated the rules hold in
.
Unless otherwise stated the rules hold in
![]() too. Recall the definition of
too. Recall the definition of
![]() from
section 3.
from
section 3.
PROOF: Let us first reduce to the case
![]() . Setting
. Setting
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
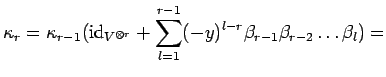
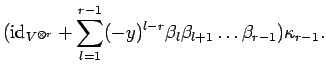
We proceed by induction on ![]() , the case
, the case ![]() being clear.
The case
being clear.
The case ![]() can be handled immediately with the help of the
above recursion formula. If
can be handled immediately with the help of the
above recursion formula. If ![]() we calculate
we calculate
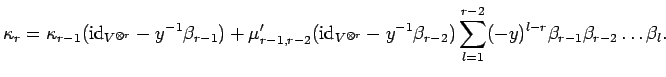
But by the braid relations we get
yielding the right hand side factorization of ![]() . The other formula
is obtained similarly.
. The other formula
is obtained similarly.
![]()
PROOF: By assumption,
![]() lies in the kernel of
lies in the kernel of
![]() . Consequently the assertion concerning
. Consequently the assertion concerning
![]() follows immediately from
Lemma 9.1 since
follows immediately from
Lemma 9.1 since
![]() .
Using the matrix transposition map
.
Using the matrix transposition map ![]() introduced in
section 8, the formula for exchanged multi-indices follows
as well.
introduced in
section 8, the formula for exchanged multi-indices follows
as well.
![]()
Next, we investigate the transition from
![]() to its epimorphic image
to its epimorphic image
![]() .
For this purpose
denote by
.
For this purpose
denote by
![]() the ideal
generated by
the ideal
generated by
![]() in the algebraic span
in the algebraic span
![]() of the endomorphisms
of the endomorphisms ![]() and
and
![]() . By equation (1) the realtion
. By equation (1) the realtion
![]() holds in
holds in
![]() . By the
braid relations
. By the
braid relations
![]() the relations
the relations
![]() and
and
![]() must hold
in
must hold
in
![]() for all
for all ![]() as well.
The Iwahori-Hecke algebra
as well.
The Iwahori-Hecke algebra
![]() of type
of type ![]() is defined
on generators
is defined
on generators ![]() for
for
![]() by relations
by relations
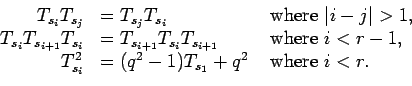
Therefore,
there is an epimorphism from
![]() to
the quotient
to
the quotient
![]() sending the generator
sending the generator ![]() to
to
![]() (notation as in [DD]).
(notation as in [DD]).
PROOF: We have to show that
![]() for all
for all
![]() . Let
. Let
![]() be such
that
be such
that ![]() . From the defining equation of the quantum coefficient
of dilation
. From the defining equation of the quantum coefficient
of dilation ![]() from section 4 we have
from section 4 we have

This means
![]() in
in ![]() for all
for all
![]() . By (5) we have
. By (5) we have
![]() and therefore,
and therefore,
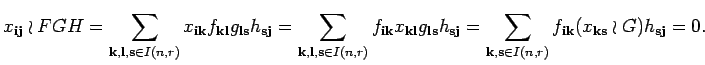
where
![]() ,
,
![]() and
and
![]() are the coefficient matrices of
are the coefficient matrices of ![]() and
and ![]() .
.
![]()
We extend the notation introduced in
(2). Let
![]() be an endomorphism of
be an endomorphism of
![]() . Set
. Set
Similar expressions are used with respect to the capital ![]() notation for bideterminants.
notation for bideterminants.
PROOF: Modulo
![]() we have
we have
since the corresponding equations (where ![]() is replaced by
is replaced by
![]() )
hold in the Iwahori-Hecke algebra
)
hold in the Iwahori-Hecke algebra
![]() .
Thus the assertion follows from Lemma 9.3.
.
Thus the assertion follows from Lemma 9.3.
![]()
Let
![]() denote the ideal in the tensor algebra
denote the ideal in the tensor algebra
![]() generated by the twofold invariant
tensor
generated by the twofold invariant
tensor
![]() and let
and let
![]()
![]() be
its
be
its ![]() -th homogeneous summand.
-th homogeneous summand.
PROOF: Since
![]() and
and
![]() for all
for all
![]() with
with ![]() by section 4 it follows that
by section 4 it follows that ![]() is contained in
is contained in
![]() . The verification of the opposite inclusion can be reduced to consider
elements of the form
. The verification of the opposite inclusion can be reduced to consider
elements of the form
![]() with
with
![]() for some
for some
![]() . But such an element can be
written as
. But such an element can be
written as
![]() for some
for some
![]() . Thus the assertion follows.
. Thus the assertion follows.
![]()
PROOF: First, note that the second equation follows from the first one by definition
of bideterminants.
By the above lemma we can reduce to the case
![]() where
where
![]() and
and
![]() . Thus we get
. Thus we get
![]()
![]()
Next, we give a quantum symplectic version of Laplace duality. The corresponding classical result can be found in [Ma, 2.5.1], for instance.
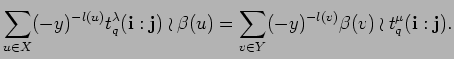
PROOF: Using the disjoint union
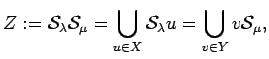
and the fact
![]() ,
,
![]() which holds by length additivity
we calculate
which holds by length additivity
we calculate
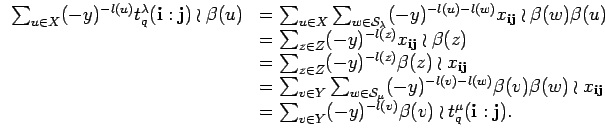
The next result is needed for the transition from
![]() -bideterminants of compositions
to
-bideterminants of compositions
to ![]() -bideterminants of
partitions.
-bideterminants of
partitions.
PROOF: First, there is a permutation
![]() , such that
, such that
![]() is a partition. This
is a partition. This
![]() is uniquely determined by
is uniquely determined by ![]() (but
(but ![]() only under the restriction to be of minimal length).
Clearly the parabolic subgroups
only under the restriction to be of minimal length).
Clearly the parabolic subgroups
![]() and
and
![]() in
in
![]() are conjugate to each other. Thus, there
is an element
are conjugate to each other. Thus, there
is an element
![]() such that
such that
![]() . Furthermore, it is known
from the theory of parabolic subgroups that in the left coset
. Furthermore, it is known
from the theory of parabolic subgroups that in the left coset
![]() and in the right coset
and in the right coset
![]() there are unique representatives
there are unique representatives ![]() (resp.
(resp. ![]() )
of minimal length. Since we have
)
of minimal length. Since we have
![]() for all
for all
![]() and
and
![]() for all
for all
![]() , we have
, we have
![]() .
By the definition of bideterminants
(
.
By the definition of bideterminants
(
![]() ),
the relations (5)
holding inside
),
the relations (5)
holding inside
![]() and the calculus for the symbol
and the calculus for the symbol ![]() given in
(3) we obtain
given in
(3) we obtain
Since
![]() this results in
this results in
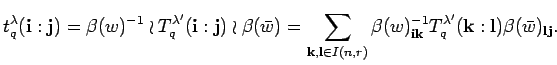
Next, we introduce a calculus for our bideterminants bringing
our special order ![]() on
on ![]() into the picture. First,
some new notation has to be explained. The sum of two
multi-indices
into the picture. First,
some new notation has to be explained. The sum of two
multi-indices
![]() and
and
![]() is
defined by juxtaposition, that is
is
defined by juxtaposition, that is
Note that the map
![]() occurring in
Theorem 8.3
is additive in the sense
occurring in
Theorem 8.3
is additive in the sense
![]() . This implies
. This implies
with respect to the lexicographic order ![]() on
on
![]() .
To a multi-index
.
To a multi-index
![]() we consider the following
we consider the following ![]() -spans
in
-spans
in
![]() :
:
Furthermore, we set
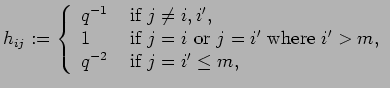
and denote the simple transpositions by
![]() , as before.
The following lemma is the key concerning calculations with bideterminants.
Again we set
, as before.
The following lemma is the key concerning calculations with bideterminants.
Again we set ![]() .
.
PROOF: The congruence relation for
![]() follows from the one for
follows from the one for ![]() because
because
![]() by (1).
Therefore, it is enough to prove the first assertion.
by (1).
Therefore, it is enough to prove the first assertion.
First, consider the case
![]() . If
. If
![]() ,
the asserted congruence relation is also an equation, as can be seen directly
from the definition of
,
the asserted congruence relation is also an equation, as can be seen directly
from the definition of ![]() . Turning to the case
. Turning to the case
![]() , we split
, we split ![]() into three summands
into three summands
To
![]() we set
we set
![]() and calculate
and calculate
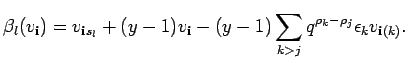
Since
![]() we obtain the equation
we obtain the equation
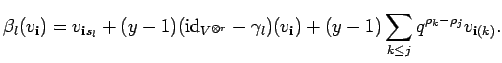
But
![]() and
and
for all ![]() by (11), yielding the asserted congruence
modulo
by (11), yielding the asserted congruence
modulo
![]() . If
. If
![]() the interesting case is
the interesting case is
![]() . Here the assertion immediately follows from
the calculation
. Here the assertion immediately follows from
the calculation
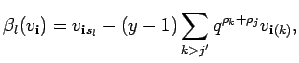
because
![]() for all
for all ![]() .
.
![]()
 if
if 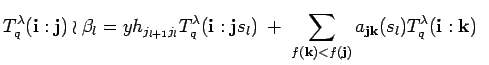 if
if
PROOF: Note that
![]() is the
coefficient of
is the
coefficient of
![]() in the
expression
in the
expression
![]() .
By definition of bideterminants and the conventions (10)
about
.
By definition of bideterminants and the conventions (10)
about ![]() , the result follows immediately from the lemma.
, the result follows immediately from the lemma.
![]()
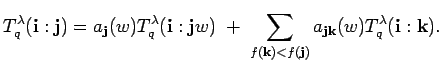
PROOF: We use induction on the length of ![]() .
If this is zero there is nothing to prove.
If not, we write
.
If this is zero there is nothing to prove.
If not, we write
![]() where
where
![]() and
and
![]() .
By the induction hypothesis we have
.
By the induction hypothesis we have
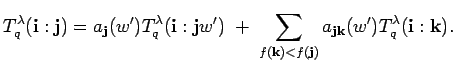
Here we have set
![]() ,
where the product runs over all pairs
,
where the product runs over all pairs
![]() such that
such that
![]() .
.
PROOF: We use induction on ![]() , the case
, the case ![]() being trivial.
For
being trivial.
For ![]() we embed
we embed
![]() as the parabolic subgroup of
as the parabolic subgroup of
![]() generated by
generated by
![]() , which fix
, which fix ![]() .
If
.
If
![]() there is nothing to prove by the induction
hypothesis. Otherwise, we write
there is nothing to prove by the induction
hypothesis. Otherwise, we write
![]() where
where
![]() and
and
![]() for an appropriate
for an appropriate ![]() , thus
, thus
![]() . By the induction hypothesis, Lemma 9.9
and Remark 9.10 we calculate
. By the induction hypothesis, Lemma 9.9
and Remark 9.10 we calculate
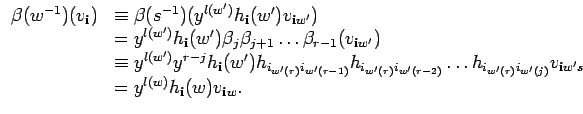
![]()

PROOF: As for the proof of Corollary 9.11, this follows
easily from the preceding lemma, Lemma ![]() and the definition of bideterminants.
and the definition of bideterminants.
![]()