Let ![]() be even. We will apply the FRT-construction to two
endomorphisms
be even. We will apply the FRT-construction to two
endomorphisms
![]() . In order to define them we have to introduce some notation.
First consider the involution
. In order to define them we have to introduce some notation.
First consider the involution
![]() on
on ![]() , that is
, that is
Further set ![]() if
if ![]() and
and
![]() if
if ![]() and define
and define

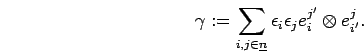
The first endomorphism is just the flip operator on ![]() , whereas the second is an integer multiple of a projection
map whose kernel is just the kernel of the linear form on
, whereas the second is an integer multiple of a projection
map whose kernel is just the kernel of the linear form on
![]() corresponding to the canonical skew bilinear form on
corresponding to the canonical skew bilinear form on
![]() (see below) and whose image is the one dimensional span of a
skew bivector. Our object of interest will be the FRT-construction
(see below) and whose image is the one dimensional span of a
skew bivector. Our object of interest will be the FRT-construction
According to the preceeding section it is a graded matric bialgebra whose homogenous summands
are the centralizer coalgebras of algebras ![]() which are generated by endomorphisms
which are generated by endomorphisms
for
![]() . Using the notation of [We] the
Brauer centralizer algebra
. Using the notation of [We] the
Brauer centralizer algebra ![]() (
(![]() an element in
an element in ![]() )
is generated by symbols
)
is generated by symbols ![]() and
and ![]() for
for
![]() and
the assignment
and
the assignment
![]() and
and
![]() defines
a representation of
defines
a representation of ![]() on
on ![]() . Thus
. Thus ![]() is
just the image of
is
just the image of ![]() under this representation, in
H. Wenzl's notation from [We]:
under this representation, in
H. Wenzl's notation from [We]:
![]() .
R. Brauer showed in [Br] that this is just the
centralizer algebra of the symplectic group
.
R. Brauer showed in [Br] that this is just the
centralizer algebra of the symplectic group
![]() acting on
acting on ![]() if
if
![]() . One of our
aims is to generalize this to the case of an arbitrary algebraically
closed field
. One of our
aims is to generalize this to the case of an arbitrary algebraically
closed field ![]() instead of
instead of ![]() .
.
Another problem, connected with the former, is
to show that the centralizer algebra ![]() of
of ![]() which will turn out
to be the symplectic Schur algebra
which will turn out
to be the symplectic Schur algebra ![]() defined by
S. Donkin in [Do2] is stable under base changes. In view of
theorem 4.3 this is equivalent to the projectivity
of the coalgebra
defined by
S. Donkin in [Do2] is stable under base changes. In view of
theorem 4.3 this is equivalent to the projectivity
of the coalgebra
![]() as an
as an ![]() -module. For this purpose
we are going to construct a basis for the latter one.
The procedure follows [Oe]
where the more general quantum case is treated. But it will become more
transparent in the much simpler classical case. First note that there is an
epimorphism of graded bialgebras from
-module. For this purpose
we are going to construct a basis for the latter one.
The procedure follows [Oe]
where the more general quantum case is treated. But it will become more
transparent in the much simpler classical case. First note that there is an
epimorphism of graded bialgebras from
to
![]() leaving the symbols
leaving the symbols ![]() fixed (we use
fixed (we use ![]() as symbols for residue classes of
as symbols for residue classes of
![]() in all cases of matric bialgebras).
For
in all cases of matric bialgebras).
For ![]() is just the
FRT-construction
is just the
FRT-construction
![]() where the relations coming from the
endomorphism
where the relations coming from the
endomorphism ![]() are omitted. This is because
are omitted. This is because
![]() just give the ordinary
commutativity relations. The kernel of this bialgebra epimorphism is the ideal
in
just give the ordinary
commutativity relations. The kernel of this bialgebra epimorphism is the ideal
in ![]() which is generated by the polynomials
which is generated by the polynomials
![]() where
where
![]() . To write down
these polynomials explicitly let us fix some notation:
. To write down
these polynomials explicitly let us fix some notation:
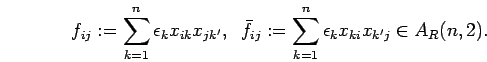
Setting ![]() and
and ![]() we obtain
we obtain

Therefore we have
where
![]() is the ideal in
is the ideal in ![]() generated by the set
generated by the set
in
![]() called the symplectic monoid by S. Doty
[Dt] and which has been
considered by D.J. Grigor'ev [Gg] first.
Here
called the symplectic monoid by S. Doty
[Dt] and which has been
considered by D.J. Grigor'ev [Gg] first.
Here ![]() is the Gram-matrix of the canonical
skew bilinear form, that is
is the Gram-matrix of the canonical
skew bilinear form, that is
![]() where
where
![]() . The function
. The function
![]() is
called the coefficient of dilation. It is neccesarily a
regular function on
is
called the coefficient of dilation. It is neccesarily a
regular function on
![]() and already
well defined in
and already
well defined in
![]() , explicitly:
, explicitly:
Note that this is independent of
![]() by the relations in
by the relations in
![]() .
Furthermore
.
Furthermore ![]() is a group-like element of this bialgebra
(cf. [Oe] 2.1.1). The set
is a group-like element of this bialgebra
(cf. [Oe] 2.1.1). The set
![]() of invertible elements in
of invertible elements in
![]() is precisely the group
is precisely the group
![]() of symplectic similitudes. S. Doty showed in [Dt] that
of symplectic similitudes. S. Doty showed in [Dt] that
![]() in fact coincides with the Zariski-closure of
in fact coincides with the Zariski-closure of
![]() in
in
![]() . We will obtain this as an easy consequence of the results
presented below.
. We will obtain this as an easy consequence of the results
presented below.
To write down a basis for
![]() we need some combinatorics.
The set of partitions of
we need some combinatorics.
The set of partitions of ![]() is denoted by
is denoted by ![]() . It contains
subsets
. It contains
subsets
![]() which consist of partitions having not more than
which consist of partitions having not more than ![]() parts.
We write partitions as
parts.
We write partitions as ![]() -tuples
-tuples
![]() of nonnegative integers
of nonnegative integers ![]() in descending order
in descending order
![]() such that
such that
![]() . To each partition one
associates a Young-diagram reading row lengths out of the
components
. To each partition one
associates a Young-diagram reading row lengths out of the
components ![]() . For example
. For example

is associated to
![]() . The column lengths
of the diagram lead to another partition
. The column lengths
of the diagram lead to another partition
![]() called the dual of the partition
called the dual of the partition ![]() , i.e.
, i.e.
![]() .
Let
.
Let ![]() denote the symmetric group on
denote the symmetric group on ![]() symbols and
symbols and
![]() the standard Young subgroup of
the standard Young subgroup of ![]() corresponding to the partition
corresponding to the partition ![]() . This is the subgroup fixing
the subsets
. This is the subgroup fixing
the subsets
![]() of
of ![]() . In the above example
. In the above example
![]() the
standard Young subgroup of
the
standard Young subgroup of ![]() corresponding to the dual
partition
corresponding to the dual
partition ![]() fixes
fixes
![]() and
and ![]() .
.
To each partition
![]() and a pair of multi-indices
and a pair of multi-indices
![]() one defines a bideterminant
one defines a bideterminant
![]() by
by

where
![]() . These are
products of minor determinants, one factor for each column, the size
of which
correspond to the length of the column. By (13)
they can be interpreted as
elements of
. These are
products of minor determinants, one factor for each column, the size
of which
correspond to the length of the column. By (13)
they can be interpreted as
elements of
![]() , as well. We wish to
write down a basis of the latter
, as well. We wish to
write down a basis of the latter ![]() -module consisting of such
bideterminants. Since they are too large in number one needs a criterion
to single out the right ones. This can be done using
-module consisting of such
bideterminants. Since they are too large in number one needs a criterion
to single out the right ones. This can be done using
![]() -tableaux. These are constructed from the diagram of
-tableaux. These are constructed from the diagram of ![]() by inserting the components of a multi-index column by column into the
boxes. In the above example:
by inserting the components of a multi-index column by column into the
boxes. In the above example:
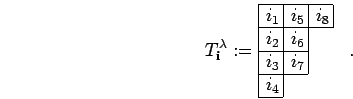
We put a new order ![]() on the set
on the set ![]() , namely
, namely
![]() .
A multi-index
.
A multi-index ![]() is called
is called ![]() -column standard if the
entries in
-column standard if the
entries in
![]() are strictly increasing down columns according
to this order. It is
called
are strictly increasing down columns according
to this order. It is
called ![]() -row standard if the
entries in
-row standard if the
entries in
![]() are weakly increasing along rows and
are weakly increasing along rows and
![]() -standard if it is both at the same time. We write
-standard if it is both at the same time. We write
![]() to denote the subset of
to denote the subset of ![]() consisting
of all multi-indices being
consisting
of all multi-indices being ![]() -standard. Such a multi-index
-standard. Such a multi-index
![]() is called
is called ![]() -symplectic standard if for each
index
-symplectic standard if for each
index
![]() the occurences of
the occurences of ![]() as well as
as well as ![]() in
in
![]() is limited to the first
is limited to the first ![]() rows. The corresponding subset of
rows. The corresponding subset of
![]() will be denoted by
will be denoted by
![]() .
.
The notion of symplectic standard tableaux traces back to
R.C. King [Ki] and it has appeard in a lot of work concerning
symplectic groups and their representation theory (for details see
[Do3]).
It is well known from invariant theory (cf. [Mr],
section 2.5) that the collection of all bideterminants
![]() where
where ![]() runs through
runs through
![]() and
and
![]() run through
run through
![]() form a
basis of
form a
basis of ![]() . Similarily we will prove in the next section
. Similarily we will prove in the next section
Before proving this let us have a look at some consequences. The first one generalizes theorem 9.5 (a) of [Dt] avoiding the restriction to characteristic zero. Furthermore, it contains corollary 5.5 (f) of that paper for algebraically closed fields.
PROOF: Let ![]() be the coordinate ring
of
be the coordinate ring
of
![]() and
and ![]() its
its ![]() -th homogenous summand.
In [Do2] the symplectic Schur algebra
-th homogenous summand.
In [Do2] the symplectic Schur algebra
![]() is defined as the dual algebra to the coalgebra
is defined as the dual algebra to the coalgebra ![]() .
The dimension of the latter one is given by Weyl's character formula
and therefore independent of the field
.
The dimension of the latter one is given by Weyl's character formula
and therefore independent of the field ![]() (cf. [Do2] p. 77).
On the other hand there is an epimorphism of graded bialgebras from
(cf. [Do2] p. 77).
On the other hand there is an epimorphism of graded bialgebras from
![]() to
to ![]() since
since
![]() is closed in
is closed in
![]() and
the latter one has been defined as the vanishing set of the ideal
and
the latter one has been defined as the vanishing set of the ideal
![]() by which
by which
![]() is defined. But by our basis theorem
6.1 the dimension of
is defined. But by our basis theorem
6.1 the dimension of
![]() is independent of the
field
is independent of the
field ![]() , as well. Thus, the proof can be finished looking at the
case
, as well. Thus, the proof can be finished looking at the
case
![]() and using
Doty's theorem 9.5 (a) or alternately by a direct calculation of
and using
Doty's theorem 9.5 (a) or alternately by a direct calculation of
![]() (see proposition 7.1 below).
(see proposition 7.1 below).![]()
By theorem 4.1 we have isomorphisms
Since
![]() has been recognized to be the
coordinate ring of
has been recognized to be the
coordinate ring of
![]() we may interpret the spectrum of
the ring
we may interpret the spectrum of
the ring
![]() as an integral monoid scheme
as an integral monoid scheme
![]() . Accordingly, an integral
form for the symplectic Schur algebra can be obtained as the
dual algebra
. Accordingly, an integral
form for the symplectic Schur algebra can be obtained as the
dual algebra
For a field of characteristic zero this has been proved by S. Doty,
too ([Dt] corollary 9.3. (c)). It should be remarked, that the
basis dual to ![]() together with the anti-involution defined by matrix
transposition give a cell datum for the symplectic Schur algebra
in the sense of J. Graham and G. Lehrer (cf. [Oe], 4.2.5).
Thus, its representation theory can be developed easily to the extent
of the treatment of cellular algebras in [GL].
together with the anti-involution defined by matrix
transposition give a cell datum for the symplectic Schur algebra
in the sense of J. Graham and G. Lehrer (cf. [Oe], 4.2.5).
Thus, its representation theory can be developed easily to the extent
of the treatment of cellular algebras in [GL].