Let us first reduce to showing that ![]() is a set of generators for
the
is a set of generators for
the ![]() -module
-module
![]() . This can be done by the following
proposition where notations from the proof of corollary
6.2 are used.
. This can be done by the following
proposition where notations from the proof of corollary
6.2 are used.
PROOF: We use [Do2] p. 74 ff.
First the reader may check that our definition of ![]() and
and
![]() is identical to the one given there.
According to
[Do2] and 2.2c in [Do1] we have
is identical to the one given there.
According to
[Do2] and 2.2c in [Do1] we have
where
![]() is the
irreducible
is the
irreducible
![]() module induced from
the linear character
module induced from
the linear character
![]() of the Borel subgroup
of the Borel subgroup ![]() (notations taken from [Do2]).
Here
(notations taken from [Do2]).
Here ![]() runs through the set
runs through the set ![]() of dominant weights
corresponding to the irreducibles occuring in
of dominant weights
corresponding to the irreducibles occuring in ![]() . If
. If ![]() denotes
the maximal torus of
denotes
the maximal torus of
![]() we may consider the
weights
we may consider the
weights ![]() as the group-like elements in its coordinate
ring. More precisely
as the group-like elements in its coordinate
ring. More precisely
![]() is of the form
is of the form
as can be seen from the argumentation in [Do2]. Here,
![]() is a partition of
is a partition of
![]() in not more than
in not more than ![]() parts and
parts and
![]() an
integer. Restricting to the symplectic group
an
integer. Restricting to the symplectic group
![]() we have
to set the coefficient of dilation
we have
to set the coefficient of dilation ![]() equal to
equal to ![]() . Thus the restriction of
. Thus the restriction of
![]() to the maximal torus of
to the maximal torus of
![]() is just the dominant
weight
is just the dominant
weight
for the symplectic group itself. Furthermore, it is easy to show that
restricting the
![]() -module structure of
-module structure of ![]() to
the symplectic group gives
the module
to
the symplectic group gives
the module
![]() induced from the linear
character
induced from the linear
character
![]() of the Borel subgroup
of the Borel subgroup
![]() of
of
![]() (for details see
[Oe], 3.3.3). But the dimension of the latter one is known to
be the cardinality of
(for details see
[Oe], 3.3.3). But the dimension of the latter one is known to
be the cardinality of
![]() (see [Do3]
theorem 2.3 b for instance). Thus, we obtain
(see [Do3]
theorem 2.3 b for instance). Thus, we obtain
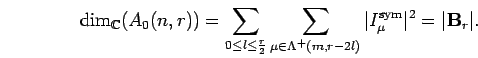
![]()
Observe that by theorem 4.1 the proof of 6.1
can be reduced to the
case
![]() , since the definition of bideterminants over
, since the definition of bideterminants over
![]() and
and ![]() respectively commutes with the isomorphism
respectively commutes with the isomorphism ![]() when
when ![]() is considered as a
is considered as a ![]() -algebra.
Now, suppose we have shown that
-algebra.
Now, suppose we have shown that ![]() generates
generates
![]() as a
as a ![]() -module.
Then the image of
-module.
Then the image of ![]() in
in ![]() under the epimorphism
considered in the proof of 6.2 is a set of
generators, too. By the above proposition it must be a basis of
under the epimorphism
considered in the proof of 6.2 is a set of
generators, too. By the above proposition it must be a basis of
![]() . Consequentely, there can't be any relations among the
elements of
. Consequentely, there can't be any relations among the
elements of ![]() , especially none with integer coefficients, giving
the desired result.
, especially none with integer coefficients, giving
the desired result.
The proof that ![]() is indeed a set of generators will follow from a
symplectic version of the famous straightening formula. For
convenience of the reader we will first state the algorithm leading to the
classical straightening formula. To do so, we put an order on the set
is indeed a set of generators will follow from a
symplectic version of the famous straightening formula. For
convenience of the reader we will first state the algorithm leading to the
classical straightening formula. To do so, we put an order on the set
![]() of partitions of
of partitions of ![]() writing
writing ![]() if the dual
if the dual ![]() occurs before the dual
occurs before the dual ![]() in the lexicographical order.
In this order the fundamental weight
in the lexicographical order.
In this order the fundamental weight
![]() is the largest element, whereas
is the largest element, whereas
![]() is the
smallest one. We abbreviate
is the
smallest one. We abbreviate ![]() and define
and define ![]() resp.
resp.
![]() to be the
to be the ![]() -linear span in
-linear span in ![]() of all
bideterminants
of all
bideterminants
![]() such that
such that ![]() resp.
resp.
![]() . For
. For
![]() we set
we set
![]() . Clearly
. Clearly
![]() .
.
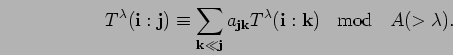
Here, the order on ![]() is the lexicographical one according to the
given order on
is the lexicographical one according to the
given order on ![]() , in our case
, in our case ![]() . A proof of the proposition can be found for
example in [Mr], 2.5.7.
. A proof of the proposition can be found for
example in [Mr], 2.5.7.
Let us now state the symplectic analogue. First consider the algebra
where
![]() is the ideal in
is the ideal in
![]() generated by the
coefficient of dilation. It is graded since
generated by the
coefficient of dilation. It is graded since ![]() is a homogenous element
but not a bialgebra because an augmentation map is missing. In fact, it turns
out that (in the case where
is a homogenous element
but not a bialgebra because an augmentation map is missing. In fact, it turns
out that (in the case where ![]() is an algebraically closed field)
it is the coordinate ring of the semigroup
is an algebraically closed field)
it is the coordinate ring of the semigroup
![]() of
noninvertible elements in the symplectic monoid (see remark
of
noninvertible elements in the symplectic monoid (see remark ![]() ).
Let us abbreviate its submodule of homogenous elements of
degree
).
Let us abbreviate its submodule of homogenous elements of
degree ![]() by
by
![]() and define
and define ![]() and
and
![]() in the same manner as above. Further,
define a map
in the same manner as above. Further,
define a map
![]() by
by
![]() , where
, where
and order
![]() writing
writing
![]() if and only if
if and only if
![]() appears before
appears before
![]() in the lexicographical order. Next, we
obtain an order
in the lexicographical order. Next, we
obtain an order ![]() on
on
![]() in a lexicographical way, as
well:
in a lexicographical way, as
well:
Finally, this gives a new order ![]() on
on ![]() via the embedding
via the embedding
![]() given by
given by
![]() . Now we are able to state the symplectic
straightening algorithm:
. Now we are able to state the symplectic
straightening algorithm:
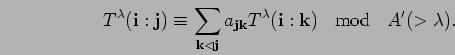
Before proving this, let us deduce that ![]() is a set of
generators for
is a set of
generators for
![]() . First note that multiplication by
the coefficient of dilation
. First note that multiplication by
the coefficient of dilation ![]() leads to an exact sequence for
leads to an exact sequence for ![]()
Therefore, by induction on ![]() we can reduce to showing that
we can reduce to showing that
is a set of generators for
![]() . For this claim it is
enough to show that
. For this claim it is
enough to show that
is a set of generators of
![]() for each partition
for each partition
![]() . This can be deduced from the straightening algorithm
7.3: Since
. This can be deduced from the straightening algorithm
7.3: Since ![]() is a finite set, the elemination of multi-indices
is a finite set, the elemination of multi-indices ![]() not being
not being
![]() -symplectic standard in an expression
-symplectic standard in an expression
![]() must terminate. This gives the straightening formula
concerning the right-hand-side argument of
must terminate. This gives the straightening formula
concerning the right-hand-side argument of
![]() :
:

Now, there is an algebra automorphism ![]() on
on ![]() induced
by matrix transposition and given by
induced
by matrix transposition and given by
![]() on
generators. Of course it is an anti-automorphism of coalgebras.
It can be readily seen that
on
generators. Of course it is an anti-automorphism of coalgebras.
It can be readily seen that
![]() and
and ![]() . Therefore, it factors to an automorphism of
. Therefore, it factors to an automorphism of
![]() which will be denoted by the same symbol. From the definition of
bideterminants we see
which will be denoted by the same symbol. From the definition of
bideterminants we see
![]() .
.
Applying ![]() to the congruence relation in
7.4 we see that
a non
to the congruence relation in
7.4 we see that
a non ![]() -symplectic standard entry
-symplectic standard entry ![]() on the left-hand-side
entry of a bideterminant can be eleminated, too, not
affecting the right-hand-side entry. Thus, it must be possible to
write
on the left-hand-side
entry of a bideterminant can be eleminated, too, not
affecting the right-hand-side entry. Thus, it must be possible to
write
![]() as a sum of bideterminants
as a sum of bideterminants
![]() modulo
modulo ![]() where
where
![]() . Therefore, the proof of
theorem 6.1 is finished as soon as proposition
7.3 is established.
. Therefore, the proof of
theorem 6.1 is finished as soon as proposition
7.3 is established.
Also, the symplectic straightening formula is related to the treatment
of symplectic Schur-modules in [Do3] and [Ia], section 6,
as can be seen from the proof of lemma 8.1 below.
Concerning the latter paper it should be noted
that the algebra
![]() defined there
as the coordinate ring of the symplectic group itself is only filtered by
defined there
as the coordinate ring of the symplectic group itself is only filtered by
![]() but not graded by
but not graded by
![]() . In fact, it can be deduced from the above
remark that
. In fact, it can be deduced from the above
remark that
![]() is the corresponding graded algebra,
that is
is the corresponding graded algebra,
that is
![]() as
as ![]() -vector spaces.
-vector spaces.