As we have seen, factoring out the submodule 
we don't cut off more
infomation as is contained in the collection of all Grothendieck
groups for fields. However, we can save additional informations,
that is, factoring out some proper submodule of instead of
if it remains
possible to define global decomposition numbers in the corresponding
quotient of 
. We now give the definition of such a one.
For each isomorphism class 
of cyclic R-modules there
is a well defined map 
to each 
given by the isomorphism class of the kernel of the
map
where I is the ideal in R such that R/I is of isomorphism type
C. Thus 
is just the isomorphism class of the R-modul
IU. It is easily seen that 
maps short split exact
sequences to short split exact sequences, such that it induces
an additive map on 
which we denote by the same symbol.
Now, if we take for U a right A-module M, then of course
is again a right A-module. Therefore one obtains
a similar additive map 
for which we will
use the same symbol as well and call it the C-residuum map.
We write 
for iterating i times and define
These are of course abelian subgroups of as the intersection
of preimages of under the additive maps 
. Later on,
we will see that they in fact are -submodules in the case where
R is a principle ideal domain. But in general this is not true.
We now define inductively a descending chain 
of -submodules. The definition
of has been given.
For i>1 let 
be the submodule of 
generated
by 
. Set
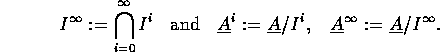
Let us illustrate this in the case of a principle ideal domain.
Then 
is of the form F=R/(p) for a prime p, that
is, [F]=[p] in the above introduced notation. We write 
for short. Since is generated by 
as a
-module we only need to calculate for prime powers 
The p-residuum of 1 and 0 is obviously 1 resp. 0. This, together
with (1) shows that 
is multiplicative, i.e.\
for 
resp.\
. Therefore, the 
are submodules in
as mentioned above, and it follows
. This means that an element
is zero in 
, iff for all 
and all primes 
you have 
. Here 
has to be defined
as the identity map.
From (1) and (3) it is easy to see that
if 
. Therefore,
implies for all primes q
if a is assumed to lie in . This shows
It should be remarked that 
is not multiplicative in general.
As an example, take the ring 
of Laurent polynomials
in the indeterminant x which is important in the context of Hecke
algebras, q-Schur algebras, Birman-Murakami-Wenzl algebras, etc.
Let 
be the Galois field to the prime 
with R-module
structure given by the natural projection. In the same
manner, 
and 
are
considered as R-modules. Then you have 
,
, and since 
it follows
